A uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
To find the pressure p inside a uniform sphere caused by gravitational compression as a function of the distance r from its center, we can follow these steps:
Step 1: Define the Density
The density ρ of the uniform sphere can be defined as:
ρ=MV=M43πR3
where M is the mass of the sphere and R is its radius.
Step 2: Consider an Elementary Volume
Consider a thin spherical shell of radius r and thickness dr. The volume dV of this shell is given by:
dV=4πr2dr
Step 3: Calculate the Mass of the Shell
The mass dm of this thin shell can be expressed as:
dm=ρ⋅dV=ρ⋅4πr2dr=⎛⎝M43πR3⎞⎠⋅4πr2dr=3MR3r2dr
Step 4: Gravitational Force on the Shell
The gravitational force dF acting on the shell due to the mass of the sphere inside it can be calculated using Newton's law of gravitation:
dF=G⋅minside⋅dmr2
where minside is the mass of the sphere of radius r:
minside=MR3r3
Thus,
dF=G⋅(MR3r3)⋅(3MR3r2dr)r2=3GM2R6r3dr
Step 5: Relate Pressure and Force
The pressure dp at radius r is related to the force dF acting on the shell:
dp=dFdA=dF4πr2
Substituting for dF:
dp=3GM2R6rdr
Step 6: Integrate to Find Pressure
To find the total pressure p at a distance r, we integrate dp from r to R:
p=∫Rrdp=∫Rr3GM2R6rdr
This gives:
p=3GM2R6(r22)Rr=3GM2R6(R22−r22)=3GM22R6(R2−r2)
Step 7: Evaluate Pressure at the Center
To find the pressure at the center of the sphere, set r=0:
p(0)=3GM22R6(R2−0)=3GM22R4
Step 8: Substitute Values for Earth
Using M≈5.97×1024kg and R≈6400×103m:
p(0)=3G(5.97×1024)22(6400×103)4
Calculating this gives:
p(0)≈1.7×1011Pa
Final Answer
The pressure p inside the sphere as a function of distance r from the center is:
p(r)=3GM22R4(1−r2R2)
And the pressure at the center of the Earth is approximately:
p(0)≈1.7×1011Pa
The density ρ of the uniform sphere can be defined as:
ρ=MV=M43πR3
where M is the mass of the sphere and R is its radius.
Consider a thin spherical shell of radius r and thickness dr. The volume dV of this shell is given by:
dV=4πr2dr
The mass dm of this thin shell can be expressed as:
dm=ρ⋅dV=ρ⋅4πr2dr=⎛⎝M43πR3⎞⎠⋅4πr2dr=3MR3r2dr
The gravitational force dF acting on the shell due to the mass of the sphere inside it can be calculated using Newton's law of gravitation:
dF=G⋅minside⋅dmr2
where minside is the mass of the sphere of radius r:
minside=MR3r3
Thus,
dF=G⋅(MR3r3)⋅(3MR3r2dr)r2=3GM2R6r3dr
The pressure dp at radius r is related to the force dF acting on the shell:
dp=dFdA=dF4πr2
Substituting for dF:
dp=3GM2R6rdr
To find the total pressure p at a distance r, we integrate dp from r to R:
p=∫Rrdp=∫Rr3GM2R6rdr
This gives:
p=3GM2R6(r22)Rr=3GM2R6(R22−r22)=3GM22R6(R2−r2)
To find the pressure at the center of the sphere, set r=0:
p(0)=3GM22R6(R2−0)=3GM22R4
Using M≈5.97×1024kg and R≈6400×103m:
p(0)=3G(5.97×1024)22(6400×103)4
Calculating this gives:
p(0)≈1.7×1011Pa
The pressure p inside the sphere as a function of distance r from the center is:
p(r)=3GM22R4(1−r2R2)
And the pressure at the center of the Earth is approximately:
p(0)≈1.7×1011Pa
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - TRY YOUR SELF33videos
GRAVITATION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - EXERCISE17videos
GRAVITATION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -I (Subjective Type Question)9videos
GRAVITATION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D9videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
Similar Questions
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution
Knowledge Check
- Question 1 - Select One
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMr - Question 2 - Select One
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
The distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionThe electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
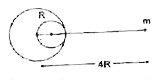 View Solution
View Solution

