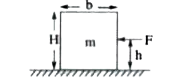
A horizontal force F is applied to applied to a homogeneous rectangular block of massm, width b and height H. The block moves with constant velocity and the coefficient of friction is μk
b2μs
bμs
b√2μs
2bμs
The correct Answer is:A
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (Matrix Matching Type Questions)
1 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (Integer Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (More than One correct answer Type Questions)
4 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A horizontal force F is applied to a homogeneous rectangular block of mass m, width b and height H. The block moves with constant velocity, the coefficient of friction is μk.
a. What is the greater height h at which the force F can be applied so that the block will slide without tipping over ?
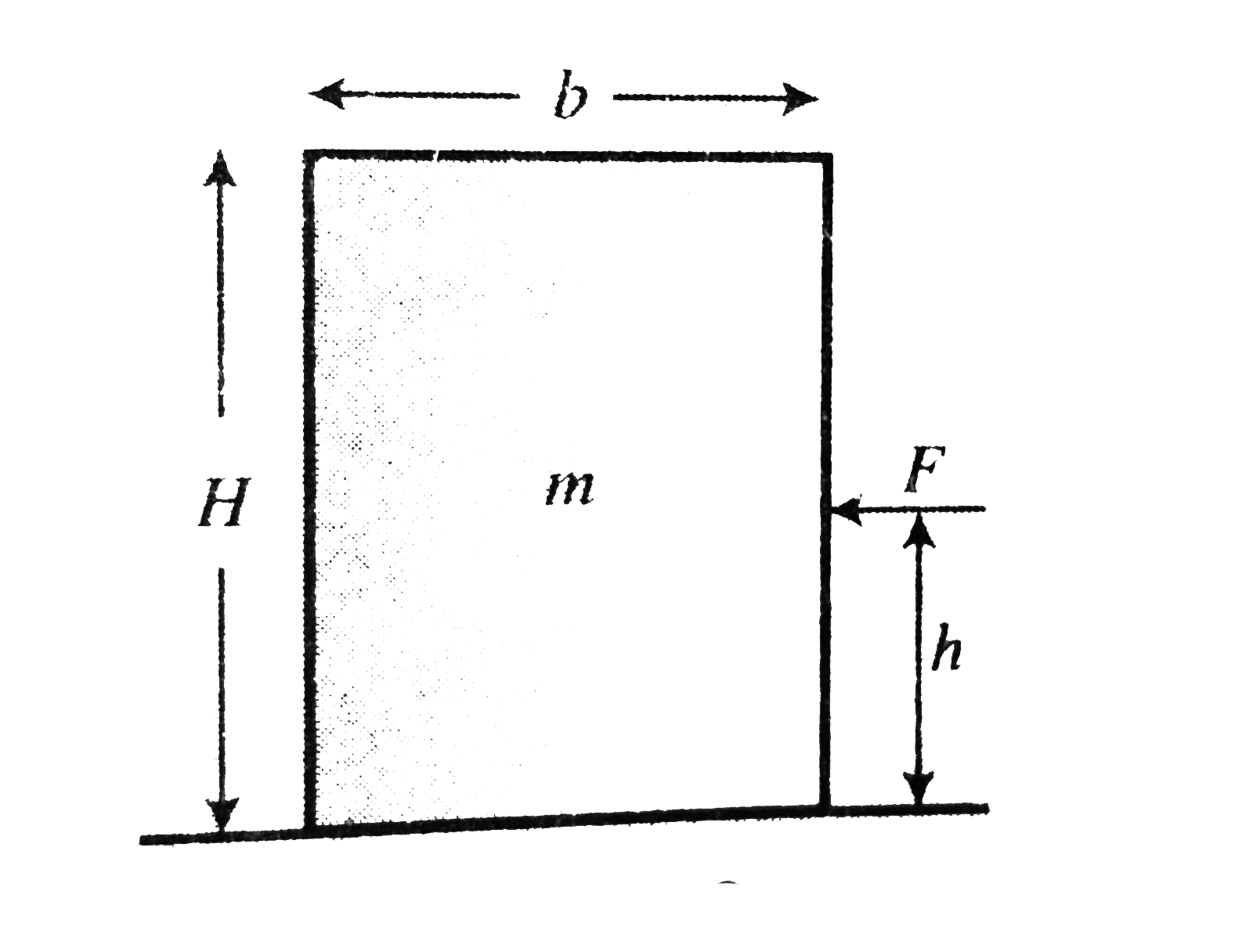
b. Through which point on the bottom face of the block will the resultant of the friction and normal forces act if h=H/2?
c. If the block is at rest and coefficient of static friction is μs what are the various criteria for which sliding or tipping occurs?
View SolutionA horizontal force F is applied to a homogeneous rectangular block of mass m, width b and height H. The block moves with constant velocity, the coefficient of friction is μk.
a. What is the greater height h at which the force F can be applied so that the block will slide without tipping over ?

b. Through which point on the bottom face of the block will the resultant of the friction and normal forces act if h=H/2?
c. If the block is at rest and coefficient of static friction is μs what are the various criteria for which sliding or tipping occurs?
View Solution
Knowledge Check
A block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
Aμmgdcosθ+μsinθBμmgdcosθcosθ+μcosθCμmgdsinθcosθ+μsinθDμmgdcosθcosθ−μsinθA homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
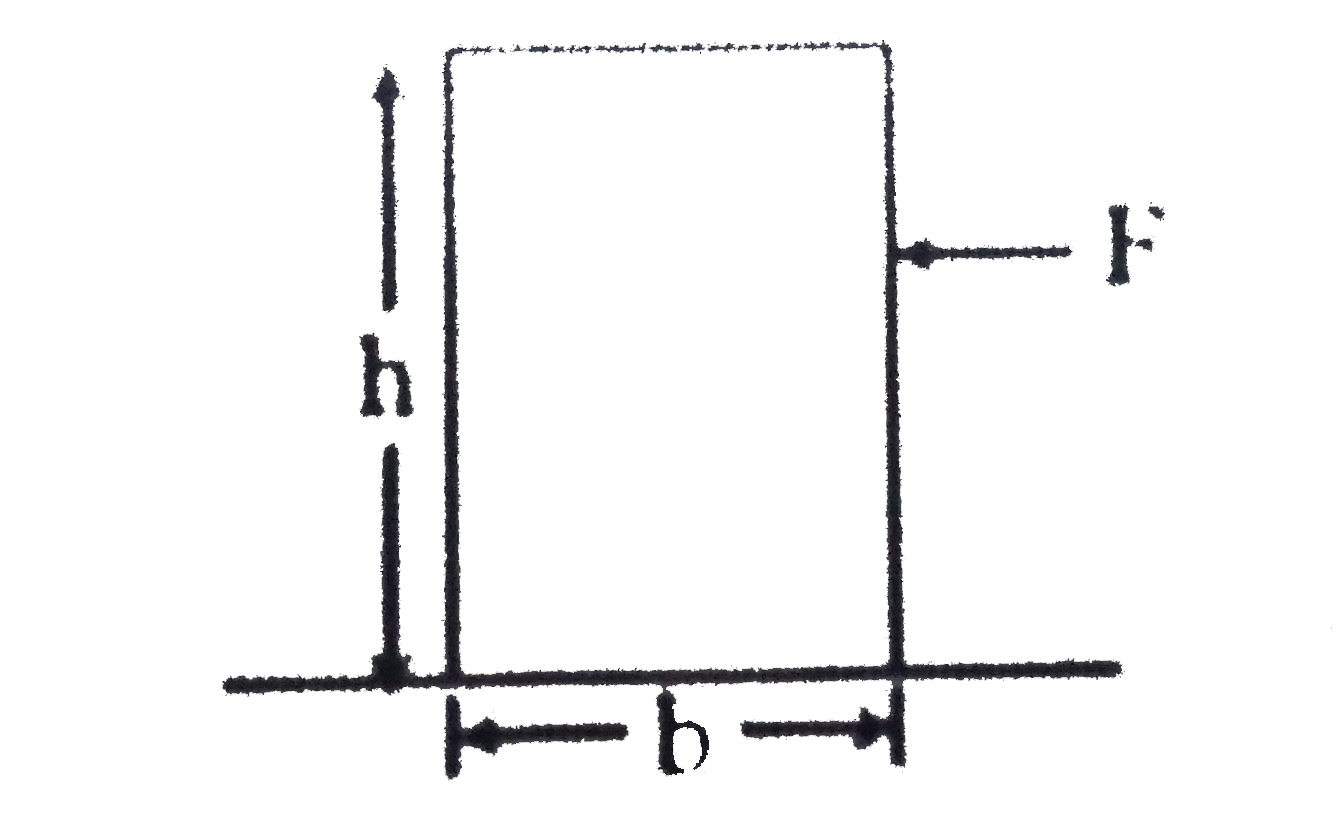 Ab2μB2bμCbμD2√2bμ
Ab2μB2bμCbμD2√2bμA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
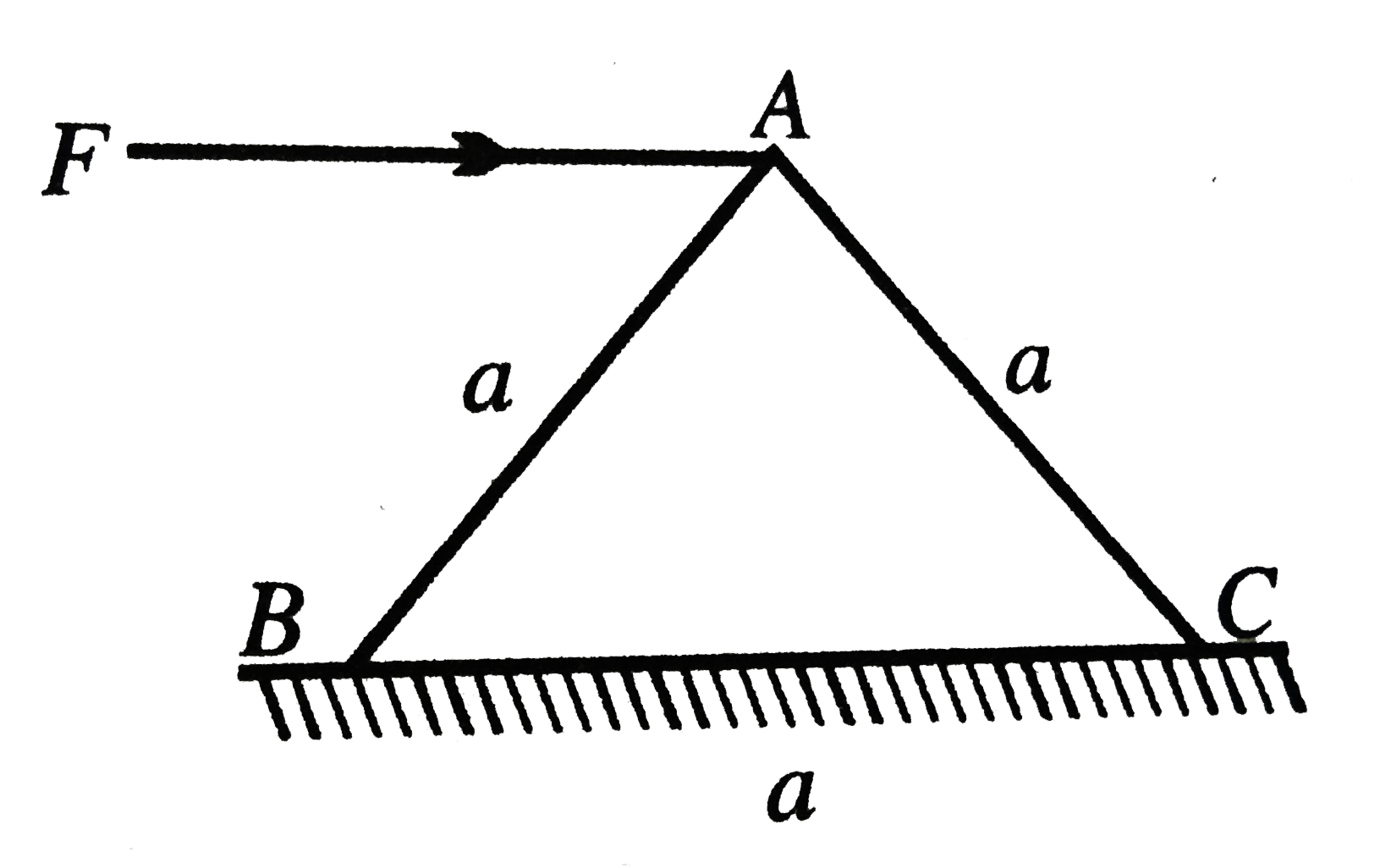 A2√3B13C1√3D12
A2√3B13C1√3D12
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ find 100μ? (√3=1.74)
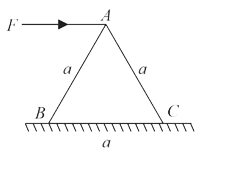
View SolutionA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ,find 100μ?(√3=1.74)
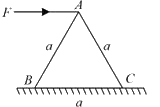
View SolutionA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be

View SolutionThe system of two blocks is at rest an shown in the figure. A variable Horizontal force is applied to the upper block. The maximum possible constant force exerted by the horizontal ground surface on the lower block is ( coefficient of friction for both the contracts is μ )
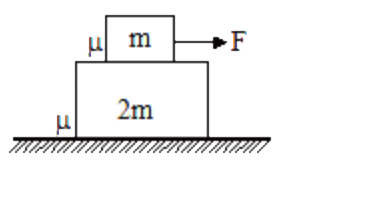
View SolutionThe system of two blocks is at rest an shown in the figure. A variable Horizontal force is applied to the upper block. The maximum possible constant force exerted by the horizontal ground surface on the lower block is ( coefficient of friction for both the contracts is μ )

View Solution
