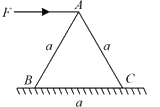
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ,find 100μ?(√3=1.74)
The correct Answer is:58
For toppling
F.a√32=mg,a2, F=mg√3
for not sliding
F≤μmg,mg√3≤μmg
μ≥1√3
Topper's Solved these Questions
Similar Questions
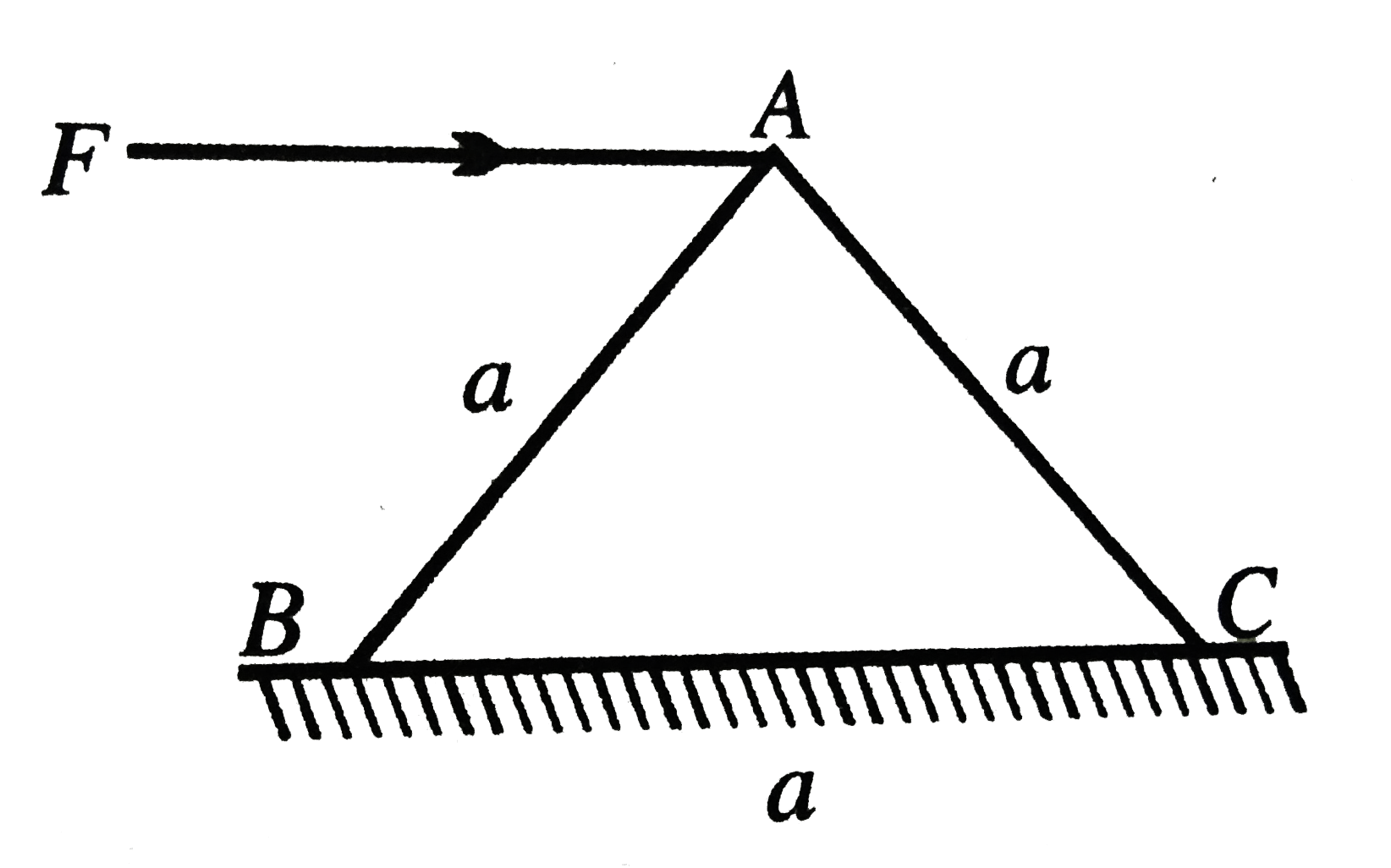
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
 View Solution
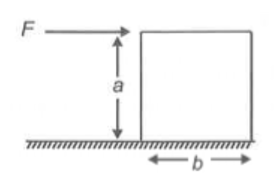
View Solutionforce F is applied at the topmost point of block of mass M. The force required to topple the block before sliding is (µ = coefficient of friction)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
AinfinitesimalBmg/4Cmg/2Dmg (−1μ) - Question 2 - Select One
A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A cubical box of side length L rests on a rough horizontal surface having coefficient of friction μ. A variable horizontal force F=αt is applied on the top of the block as shown in figure, where α is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is
 View Solution
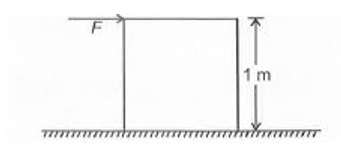
View SolutionA cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]
 View Solution
View SolutionFind value of pulling force F for which block just moves. Given coefficient of friction for surface is μ.
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
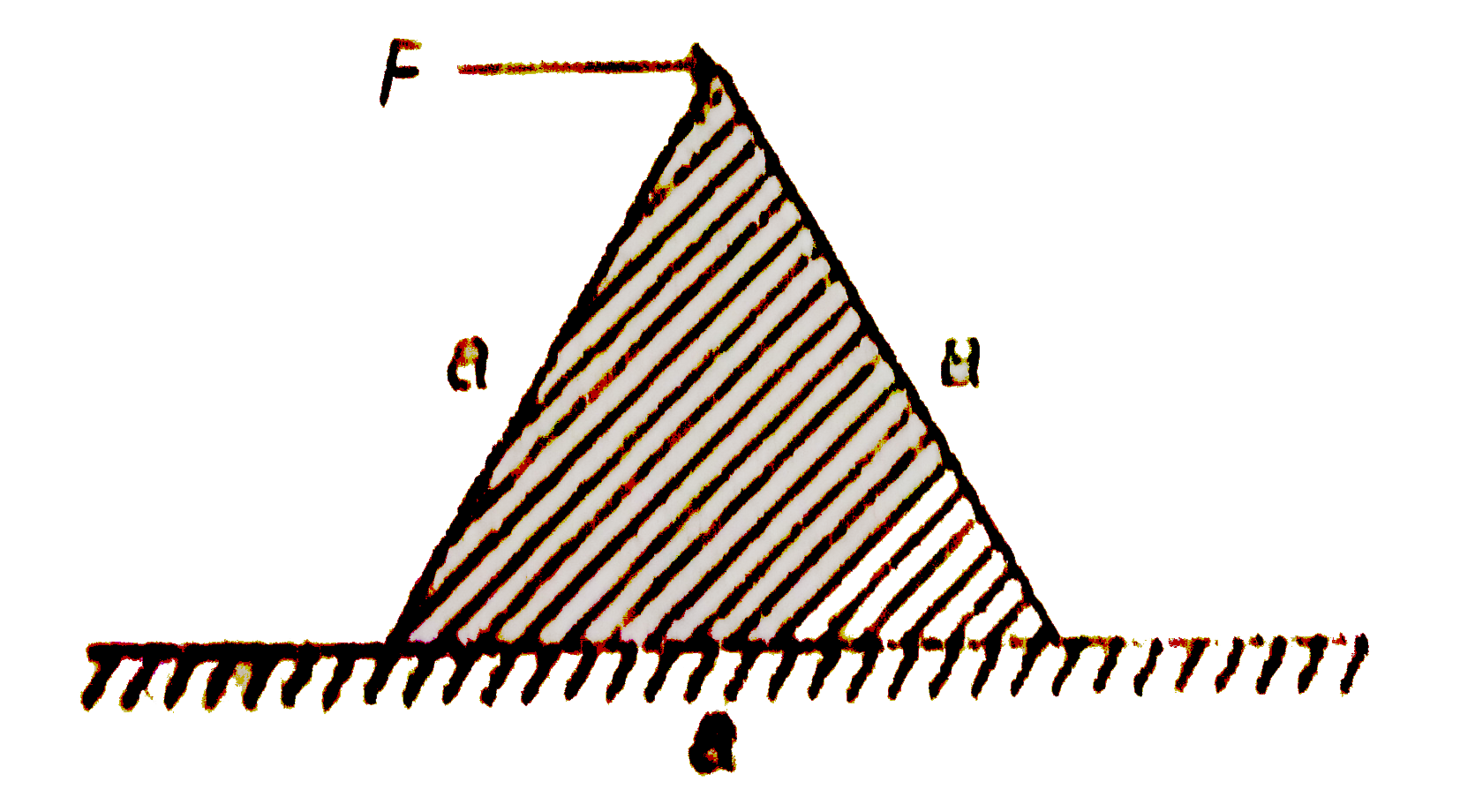 View Solution
View SolutionTwo block , with masses m1 and m2 are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle α below the horizontal . The coefficient of friction between m1 and m2 are μs
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together
 View Solution
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
View Solution

