A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel force of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is x(F+ma)lma. Where 'x' is
The correct Answer is:2
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - III) Angular Momentum (Straight Objective Type Questions)
4 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - III) Angular Momentum (More than One correct answer Type Questions)
2 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (Matrix Matching Type Questions)
1 Video
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
View SolutionA thin uniform rod of mass m=1kg moves translationally with acceleration a=2 ms−1 due to two antiparallel forces of arm-length l=20 cm . One forces is of magnitude 5 N and acts at one extreme end. Find the length of the rod.

View Solution
Knowledge Check
A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
A2(F+ma)lmaBl(1+Fma)C(F+ma)l2maDmalma+FA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of level arm I. One force is of magnitude F and acts at one extreme end. The length of the rod is
Amalma+FB2(F+ma)lmaCl(l+Fma)D(F+ma)l2maA thin uniform rod AB of mass 1kg move translationally with acceleration a=2m/s2 due to two antiparallel force as shown. If l=20cm then:
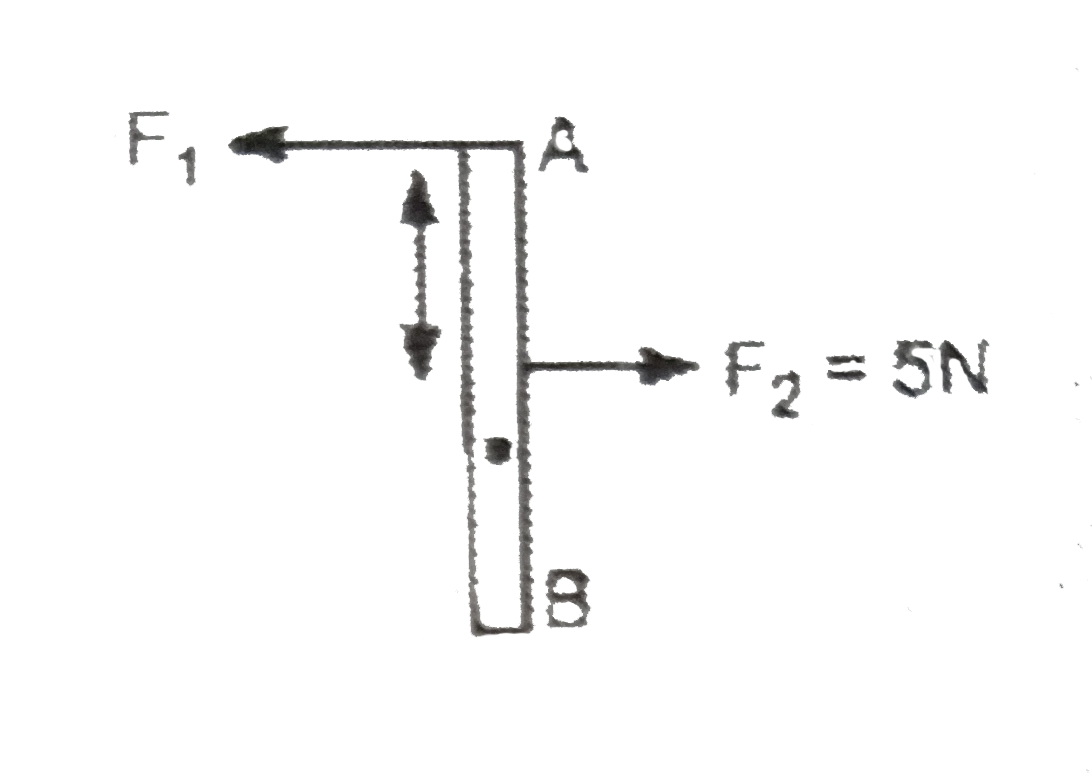 AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm
AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm
A thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
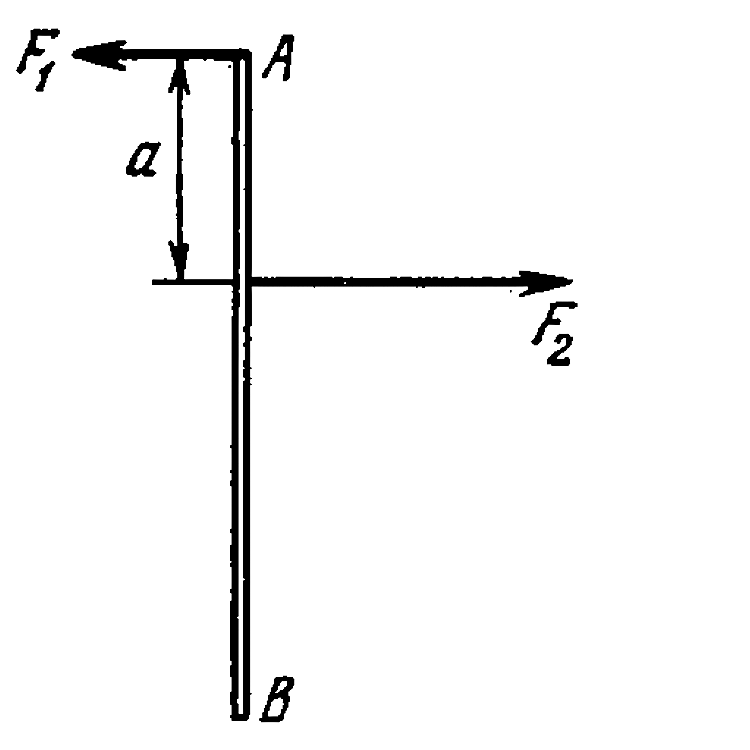
View SolutionA thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
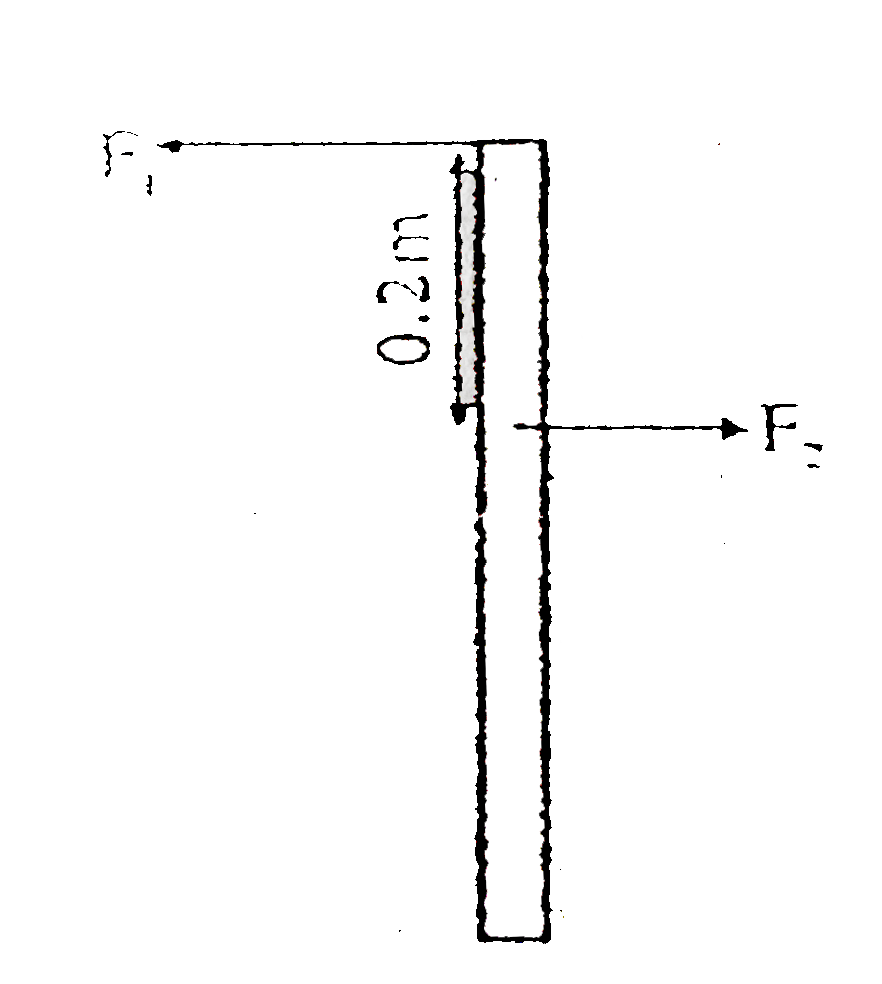
View SolutionA Thin uniform rod AB of mass m=1.0kg moves translationally with acceleration a=2.0m/s2 due to two antiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to d=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.

View Solution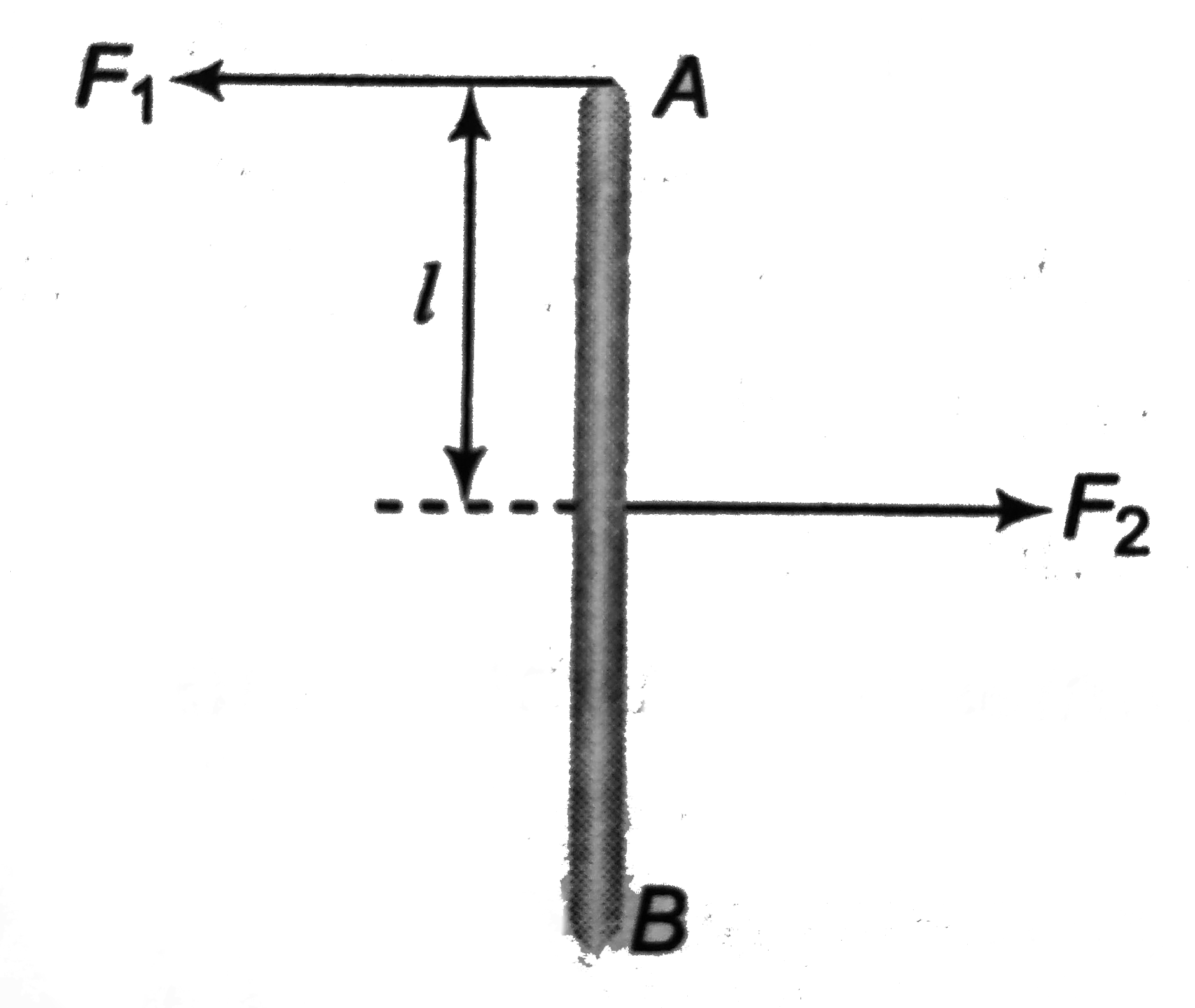
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.
View SolutionA thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
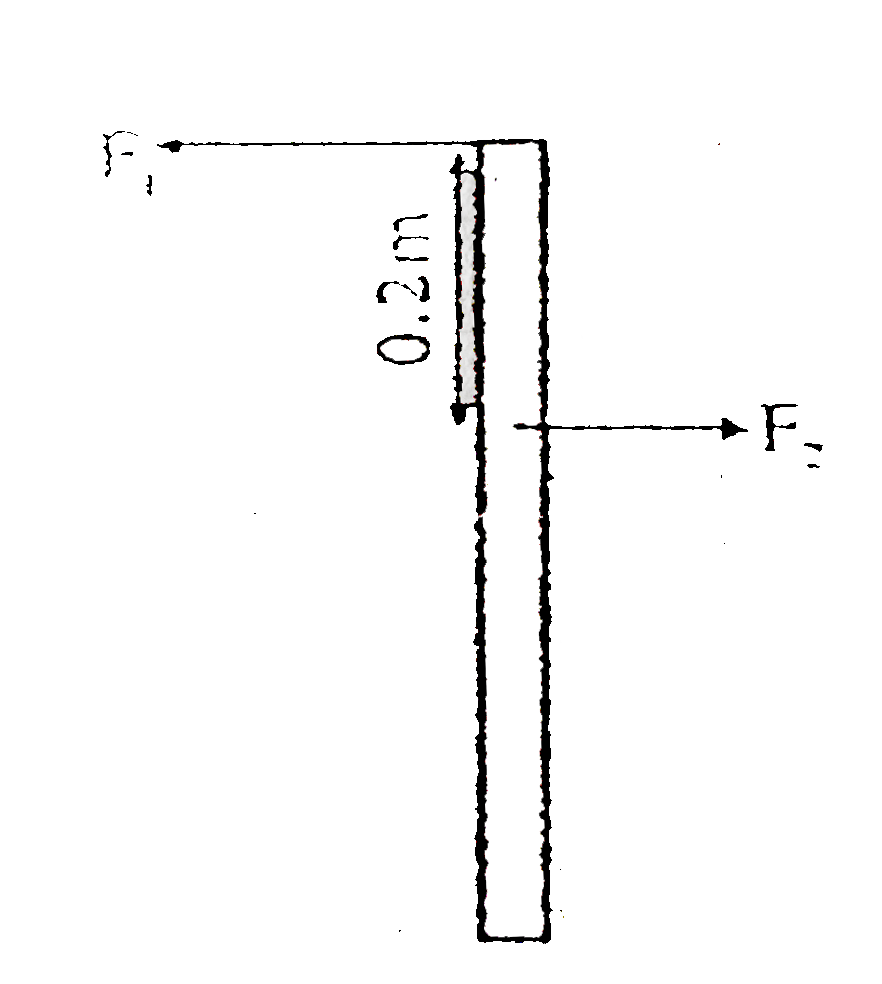
View Solution
