A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
2(F+ma)lma
l(1+Fma)
(F+ma)l2ma
malma+F
The correct Answer is:A
To solve the problem of finding the length of a thin uniform rod subjected to two antiparallel forces, we can follow these steps:
1. Identify the Forces and Setup:
- Let the rod have a mass m and a length D.
- One force F acts at one end of the rod, and the other force F′ acts at the opposite end.
- The lever arm (distance between the two forces) is given as l.
2. Apply Newton's Second Law:
- The net force acting on the rod is given by:
F′−F=ma
- Rearranging gives:
F′=F+ma
3. Calculate the Torque:
- The torque due to force F′ about the center of the rod (which is at D/2) is:
τ′=F′⋅(D2−l)
- The torque due to force F about the center of the rod is:
τ=F⋅(D2)
4. Set the Net Torque to Zero:
- Since the rod is in translational motion and not rotating, the net torque must equal zero:
τ′−τ=0
- This gives:
F′⋅(D2−l)=F⋅(D2)
5. Substituting for F′:
- Substitute F′=F+ma into the torque equation:
(F+ma)⋅(D2−l)=F⋅(D2)
6. Expand and Rearrange:
- Expand the left side:
F⋅(D2−l)+ma⋅(D2−l)=F⋅(D2)
- Rearranging gives:
ma⋅(D2−l)=F⋅l
7. Solve for the Length D:
- Isolate D:
D=2Flma+2l
8. Final Expression:
- Thus, the length of the rod D can be expressed as:
D=2(F+ma)lma
Conclusion:
The length of the rod D is given by the formula:
D=2(F+ma)lma
- Let the rod have a mass m and a length D.
- One force F acts at one end of the rod, and the other force F′ acts at the opposite end.
- The lever arm (distance between the two forces) is given as l.
- The net force acting on the rod is given by:
F′−F=ma
- Rearranging gives:
F′=F+ma
- The torque due to force F′ about the center of the rod (which is at D/2) is:
τ′=F′⋅(D2−l)
- The torque due to force F about the center of the rod is:
τ=F⋅(D2)
- Since the rod is in translational motion and not rotating, the net torque must equal zero:
τ′−τ=0
- This gives:
F′⋅(D2−l)=F⋅(D2)
- Substitute F′=F+ma into the torque equation:
(F+ma)⋅(D2−l)=F⋅(D2)
- Expand the left side:
F⋅(D2−l)+ma⋅(D2−l)=F⋅(D2)
- Rearranging gives:
ma⋅(D2−l)=F⋅l
- Isolate D:
D=2Flma+2l
- Thus, the length of the rod D can be expressed as:
D=2(F+ma)lma
The length of the rod D is given by the formula:
D=2(F+ma)lma
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Comprehension Type Questions
Explore 40 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
A thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter

View Solution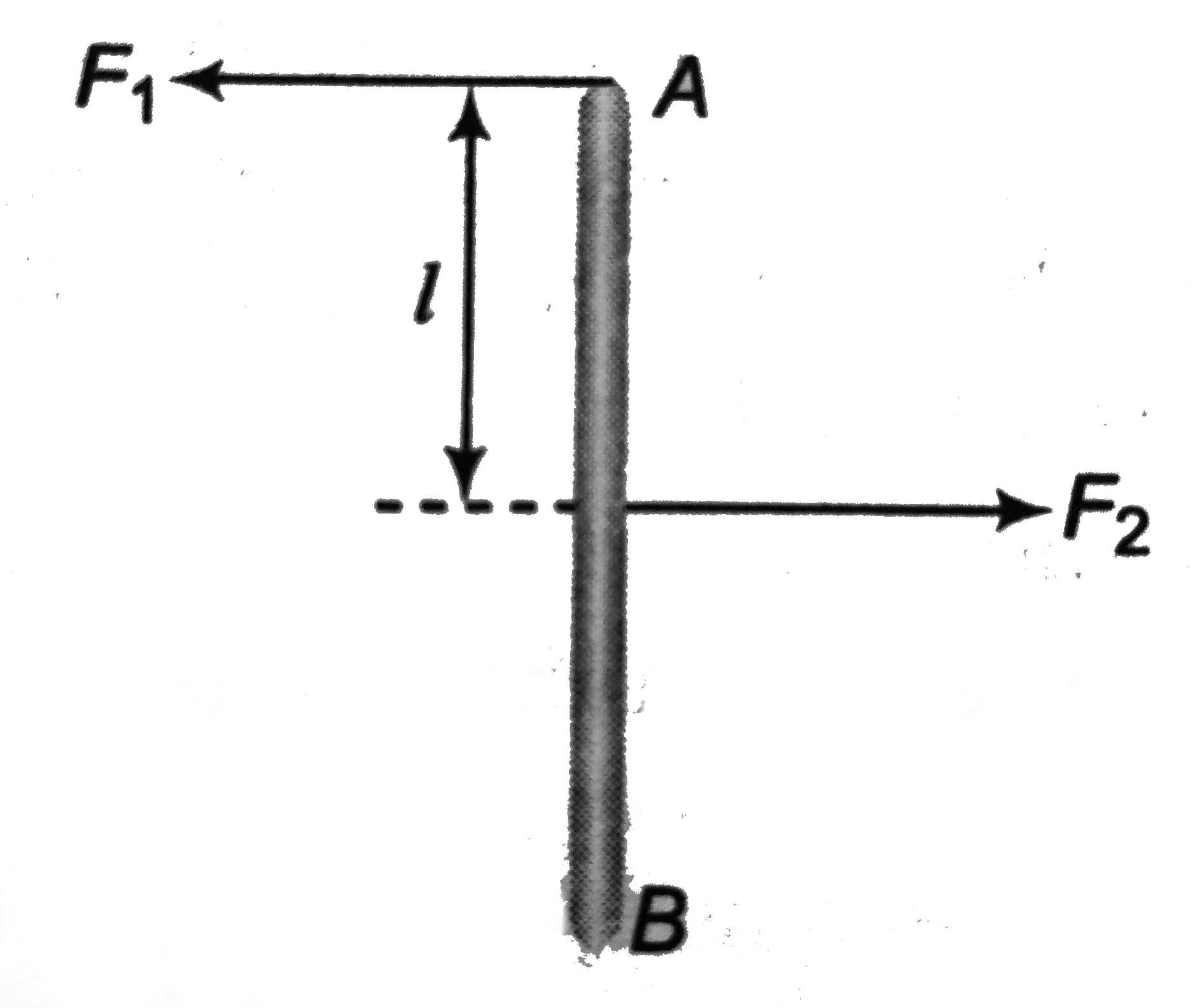
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionThe rod of length l and mass m lies on a smooth floor. A ball of mass m moving horizotally with a speed u0 striked one end of rod and stick to it. After the collision, the point on the rod that moves translationally ( without any rotation) in the previous direction of motion of the ball.

A. Is the centre of C of the rod.
B. Is the left end A of the rod.
C. Lies at a distance l/4 to the left of point C
D. Lies at a distance l/4 to the right of point C.
View SolutionA thin uniform rod of length l is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.
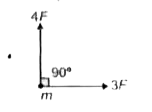
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.

View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

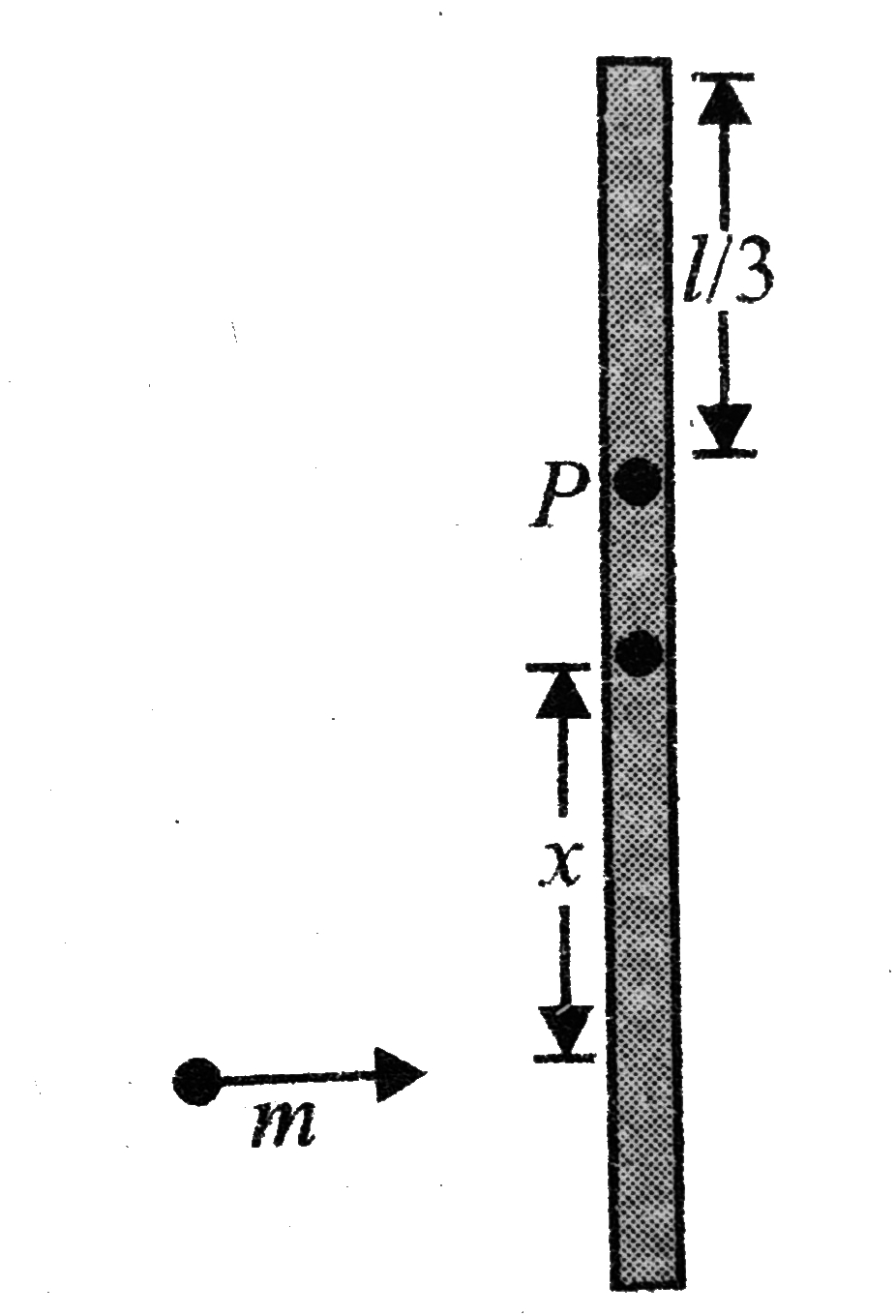
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View Solution