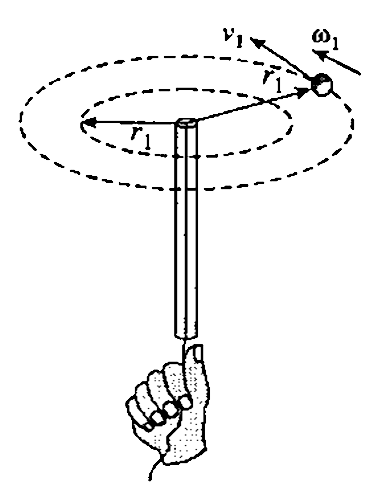
A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle of radius 2m with speed of 4 m/s. The cord is then pulled down so that the radius of the circle reduces to 1m. The ratio of kinetic energies under the final and initial state is

Text Solution

Verified by Experts

The correct Answer is:4

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - V) Angular Impulse Rod-Particle Collisions ( Straight Objective Type Questions )
3videos
ROTATIONAL DYNAMICS
BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - V) Angular Impulse Rod-Particle Collisions (More than One correct answer Type Questions )
2videos
ROTATIONAL DYNAMICS
BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - IV) Law of conservation of angular momentum (Linked Comprehension Type Questions)
3videos
ROTATIONAL DYNAMICS
BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6videos
RIVISION EXERCISE
BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20videos
ROTATIONAL MECHANICS

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
A $m g = \frac{m v^{2}}{r}$
B $m g > \frac{m v^{2}}{r}$
C $m g \leq \frac{m v^{2}}{r}$
D $m g \geq \frac{m v^{2}}{r}$
Question 2 - Select One
A small stone of mass $m$ is attached to a light string which passes through a hollow tube. The tube is held by one hand and the free end of the string by the other hand. The mass is set into revolution in a horizontal circle of radius $r_{1}$ with a speed $v_{1}$ . The string is pulled down shortening the radius of the circular path to $r_{2}$ . Which of the following is not correct? ( $ω_{1}$ and $T$ have usual meanings)
A $\frac{ω_{2}}{ω_{1}} = \frac{r_{1}^{2}}{r_{2}^{2}}$
B $\frac{E_{k 1}}{E_{k 2}} = \frac{r_{2}^{2}}{r_{1}^{2}}$
C $\frac{E_{k 1}}{E_{k 2}} = \frac{r_{2}^{2}}{r_{1}^{2}}$
D $\frac{T_{2}}{T_{1}} = \frac{r_{1}^{3}}{r_{2}^{3}}$
Question 3 - Select One
A sphere of mass m is tied to end of a string of length l and rotated through the other end along a horizontal circular path with speed v . The work done in full horizontal circle is
A0
B $(\frac{m v^{2}}{l}) .2 π l$
C $m g .2 π l$
D $(\frac{m v^{2}}{l}) . (l)$

AAKASH SERIES-ROTATIONAL DYNAMICS -LECTURE SHEET (EXERCISE - IV) Law of conservation of angular momentum (Integer Type Questions)

Home
Ask Doubt
Profile