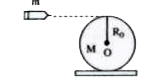
A bullet of mass m moving with velocity v strikes and becomes embedded at the edge of a cylinder of mass M and radius R0. As shown in Fig. The cylinder, initially at rest, begins to rotate about its symmetry axis, which remains fixed in position. Assuming no frictional torque, what is the angular velocity of cylinder after this collision mv(1xM+m)R0 where 'x' is
The correct Answer is:2
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - VI) (LEVEL - I Straight Objective Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - VI) (LEVEL - II More than One Correct answer Type Questions)
4 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - V) (LEVEL - II More than One correct answer Type Questions)
7 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A bullet of mass m moving with velocity v strikes and becomes embedded at the edge of a cylinder of mass M and radius R0 as shown in fig. The cylinder, initially at rest, begins to rotate about its symmetry axis, which remains fixed in position. Assuming no frictional torque, what is the angular velocity of the cylinder after this collision? Kinetic energy conseved?

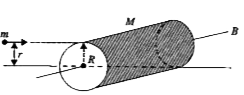
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
A62.6 J sB70.4 J sC79.6 J sD60.5 J s
A bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View SolutionWhat is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionA small body of mass 100 g moving with a velocity 2 m/s is strikes a solid cylinder of mass 2 kg and radius 20 cm. The cylinder is initially at rest and is mounted on a fixed horizontal axle that passes through the centre of mass. The line of motion of the small body is at a perpendicular lar distance of 15 cm from the centre of the cylinder. The small body strikes the cylinder and adheres to its surface. What is the angular speed of the system just after the collision ? Assume there is no friction.
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of larger disc after collision is
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of largen disc after collision is
View Solution
