An impulse J is applied on a ring of mass m along line passing through its centre O. the ring is placed on a rough horizontal durface. The linear velocity of centre of ring once it starts rolling without slipping is J/xm where 'x' is

The correct Answer is:2
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - VI) (LEVEL - I Straight Objective Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - VI) (LEVEL - II More than One Correct answer Type Questions)
4 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - V) (LEVEL - II More than One correct answer Type Questions)
7 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
An impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
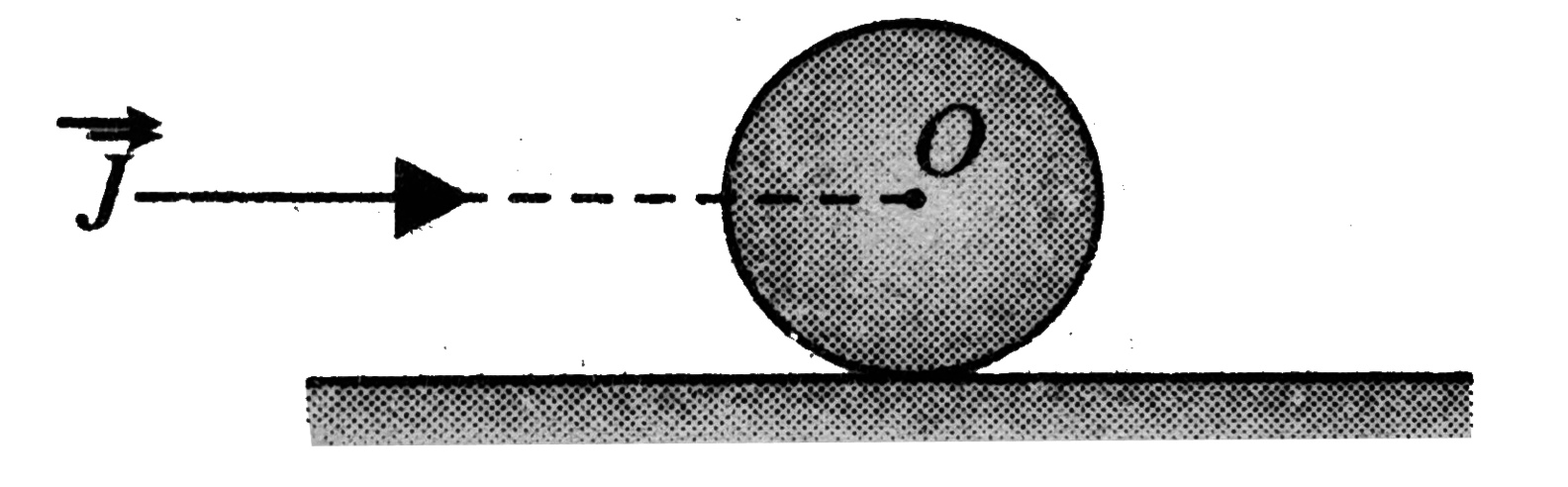
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View Solution
Knowledge Check
An impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
 AJ/mBJ/2mCJ/4mDJ/3m
AJ/mBJ/2mCJ/4mDJ/3mA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
A4×10−3 jouleB4×10−2 jouleC2×10−3 jouleD2×10−2 jouleA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZero
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

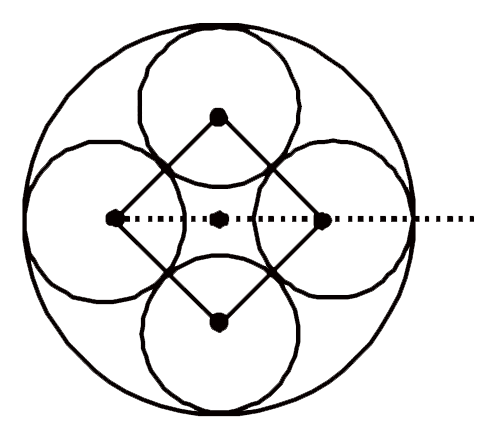
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
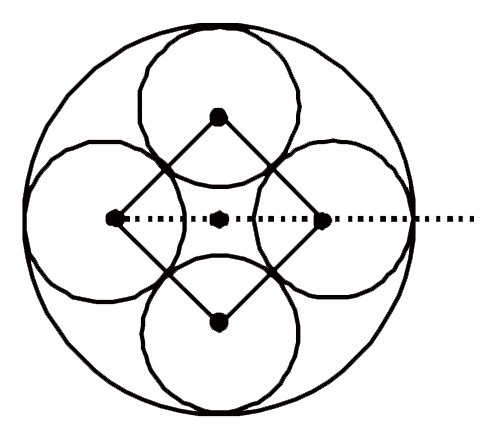
The moment of inertia of the combined ring system about the centre of ring will be
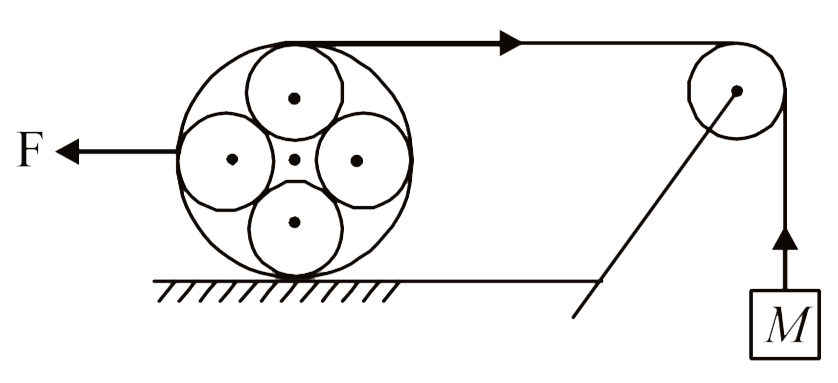
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
The magnitude of F is
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
If the masses of the spheres were doubled keeping their dimensions same, the force of friction between the ring and the horizontal surface would
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
