A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure. Immediately after the right string is cut.
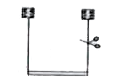
Linear accleration of the free end of the rod is 3g2
Linear accleration of the middle of the rod is 3g4
Tension in the left string is mg2
Tension in the left string is mg4
The correct Answer is:A, B, D
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Linked comprehension Type Questions
6 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-I Straight Objective Type Questions)
51 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions

A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View Solution
A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is
 Amg2B2mgCmg4Dmg
Amg2B2mgCmg4DmgA rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
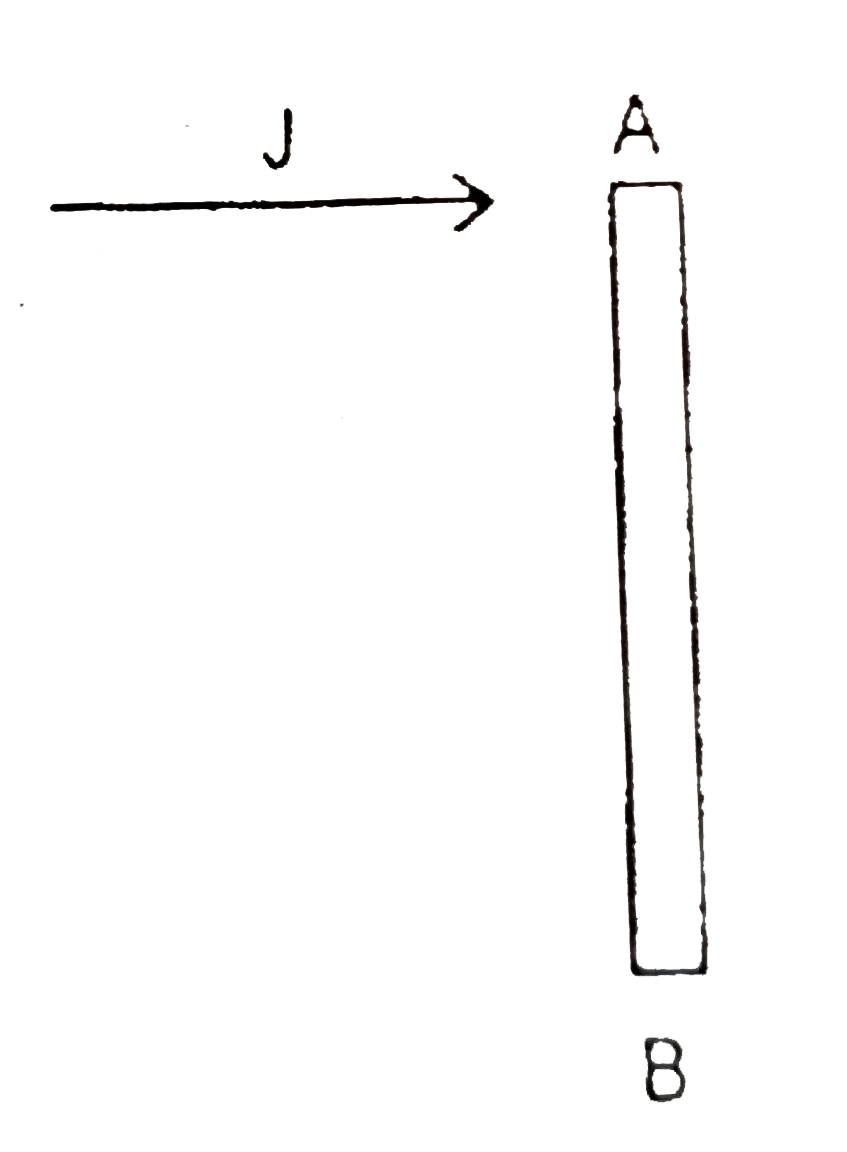 AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.
AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.A uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3
A uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View SolutionA thin uniform bar of mass m and length 2L is held at angle 30∘ with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing immediately after string breaks is

View SolutionA thin uniform bar of mass m and length 2L is held at angle 30∘ with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing the tension in the string at the left end of the bar immediately after string breaks is T=n13mg

View SolutionA thin uniform bar of mass m and length 2L is held at an angle 30∘ with the horizontal by means of two vertical inextensible strings, at each end as shown in figure. If the string at the right end breaks, leaving the bar to swing, determine the tension in the string at the left end and the angular acceleration of the bar immediately after string breaks.

View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View Solution
