A Wheel of radius 3R and mass m is placed on an inclined plane of inclination θ and a massless, inextensible string is wound around an axle of radius R as shown in figure. If the inclined plane is frictionless and string does not slip on the axle, the acceleration of the wheel tention in the string is (I=Moment of inertia of the wheel)
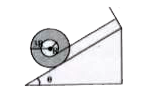
acceleration of the wheel is gsinθI+I3mR2
acceleration of the wheel is gI+I3mR2
Tension in the string mgsinθI+3mR2I
Tension in the string is mgI+3mR2I
The correct Answer is:A, C
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Linked comprehension Type Questions
6 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-I Straight Objective Type Questions)
51 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
An object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
ADecreases the rotational and translational motionBDissipates energy as heatCDecreases the rotational motionDConverts translational energy to rotational energyA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
Adecreases the rotational and translational motionBdissipates energy as heatCdecreases the rotational motionDconverts translational energy to rotational energy
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
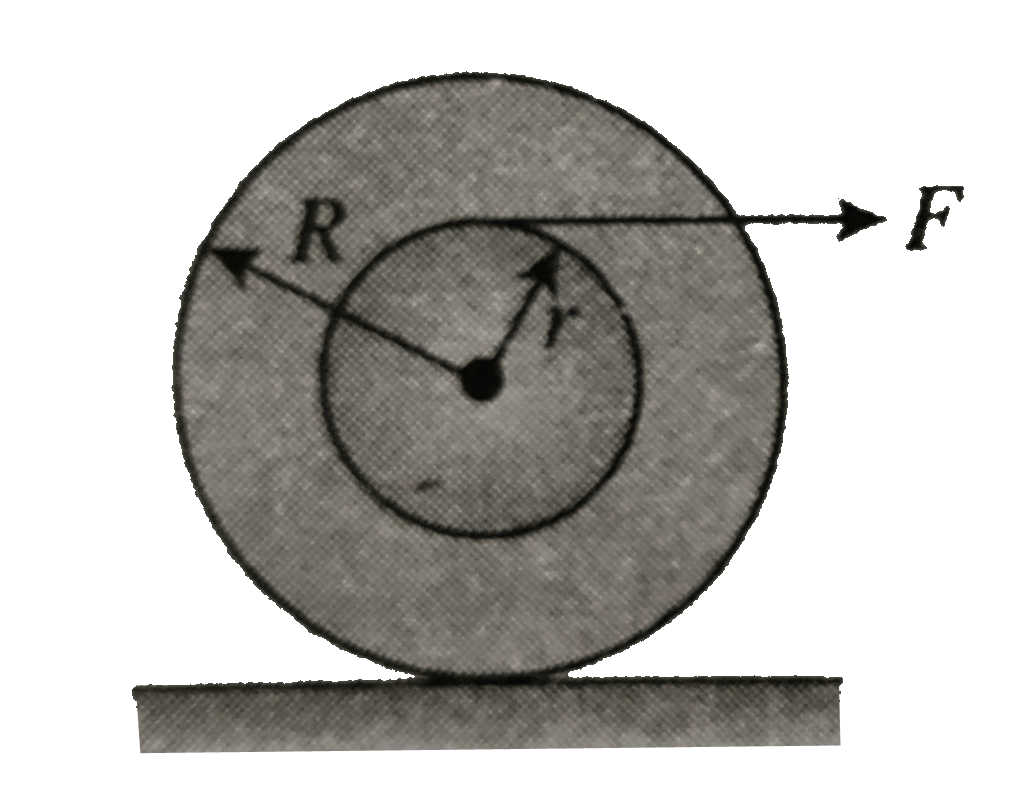
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.

a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View Solution
