Passage - VII :
A uniform rod of mass M and length 2a, can turn freely about end which is fixed. It is started with angular velocity ω from the position in which it hangs vertically.
Its angular velocity at an instant when it makes an angle θ with downward vertical is
(ω2−2g3a(1−cosθ))12
(ω2−3g2a(1−cosθ))12
(ω2+2g3a(1−cosθ))12
(ω2−3g4a(1−cosθ))12
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Matrix Matching Type Questions
2 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
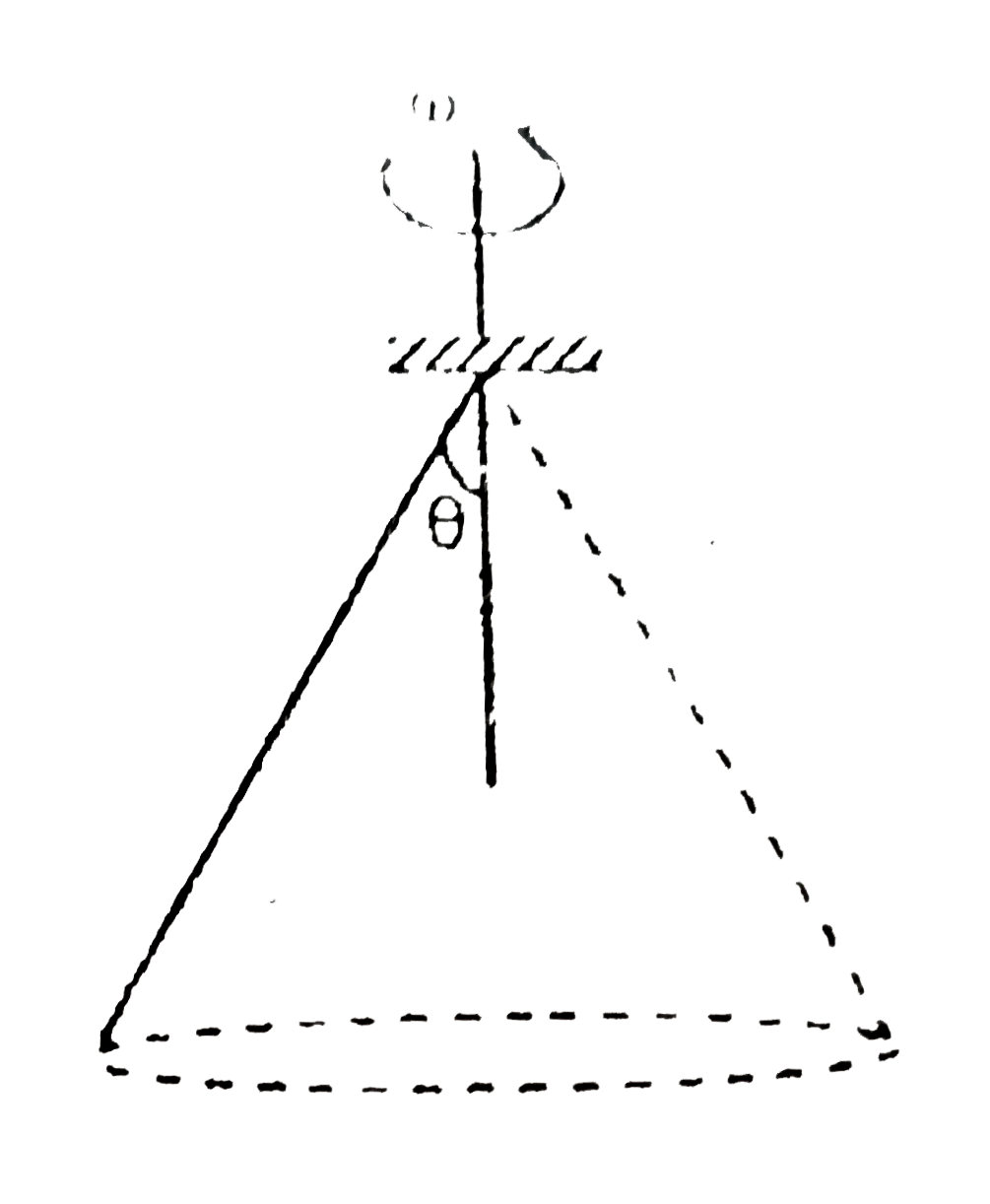
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
View SolutionA uniform rod of mass m and length L is hinged about one end and can freely rotate in a vertical plane. The angular velocity of the rod, when it falls from position P to Q. through an angle α starting from rest, is

View Solution
Knowledge Check
A uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
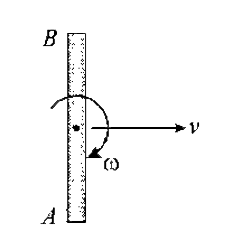 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ωA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
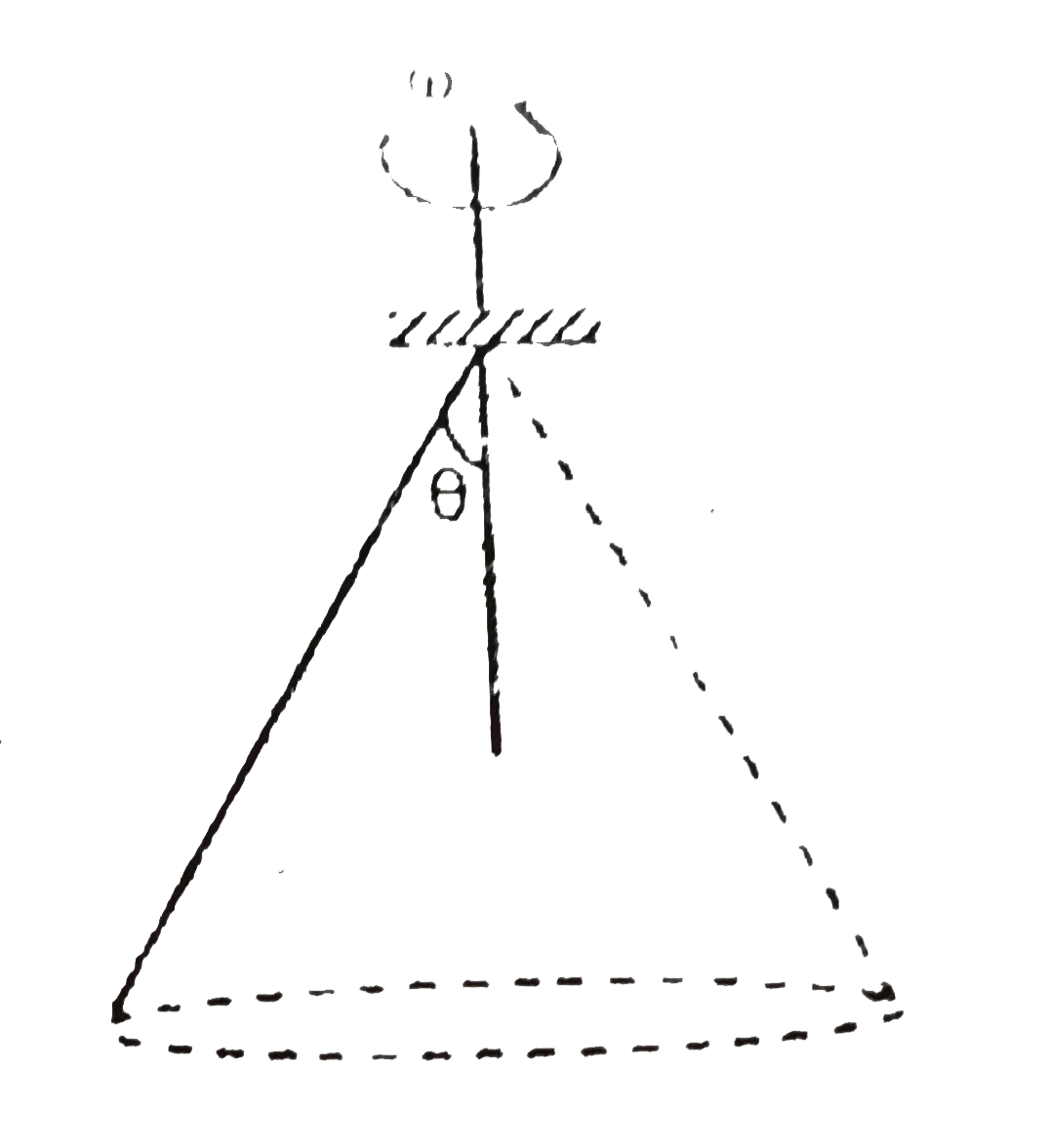 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
A rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
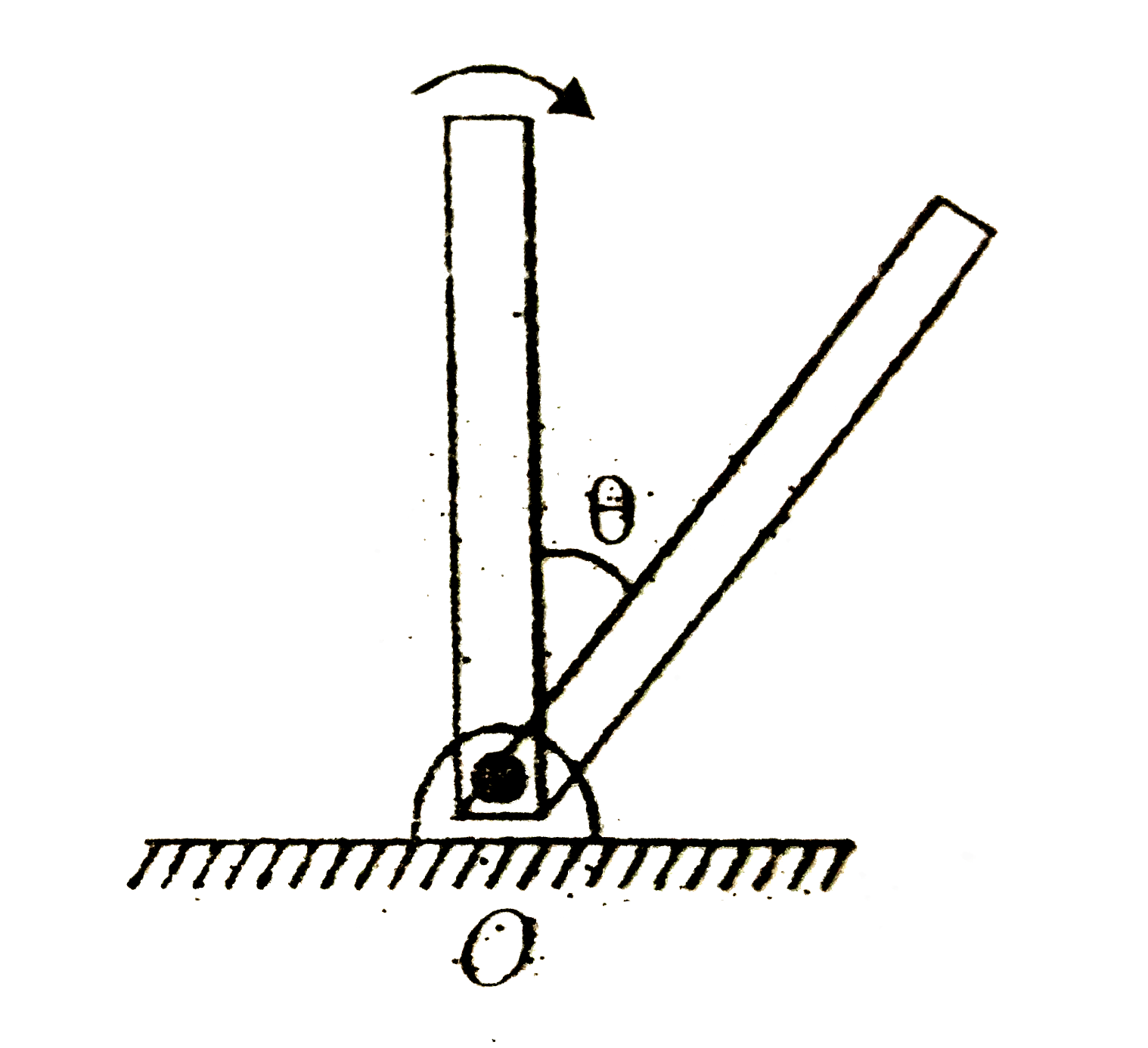
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
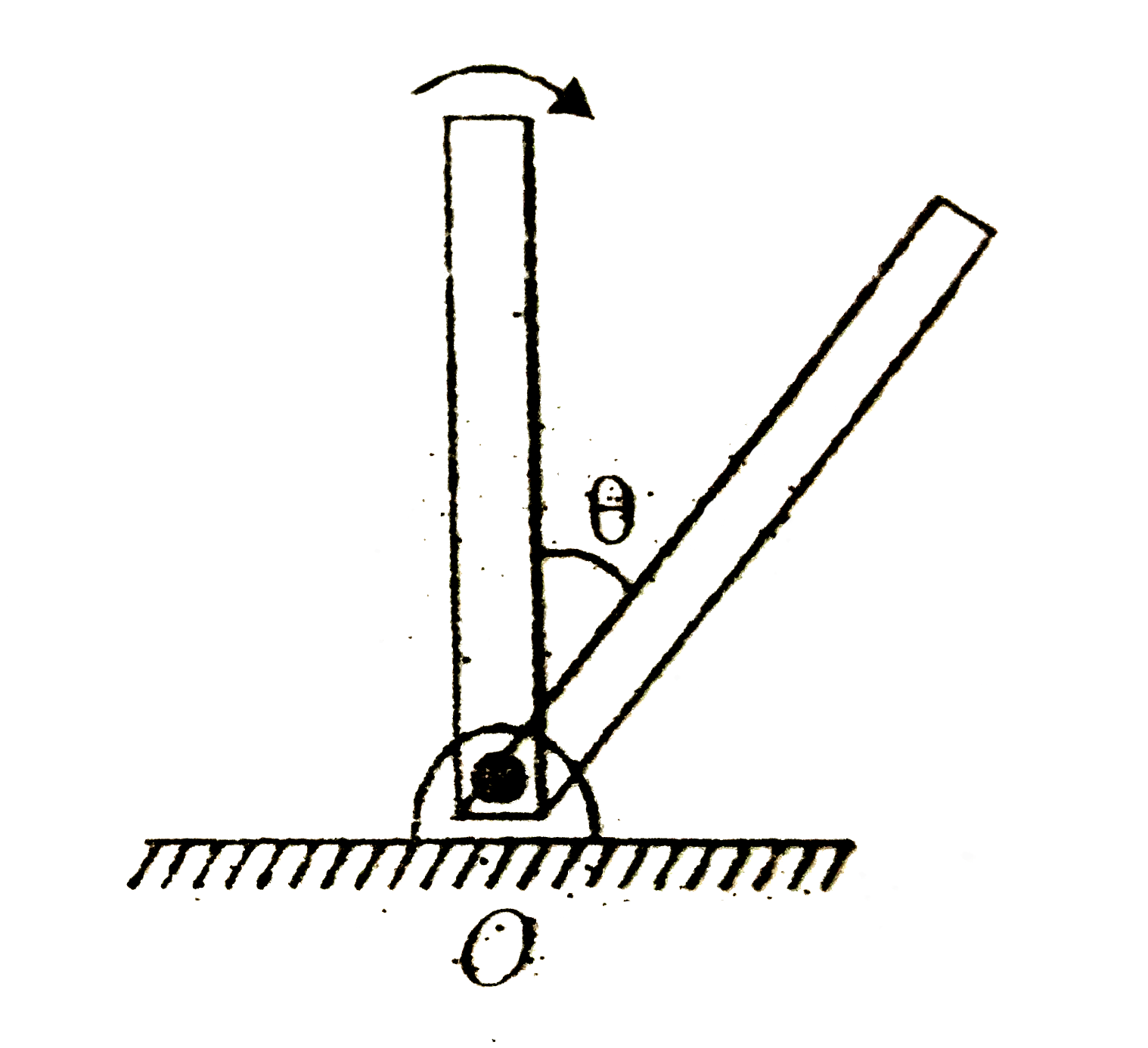
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA thin uniform rod of mass m and length l, pivoted freely at its base, is allowed to fall from a vertical position. Calcualte its angular velocity and acceleration when it has turned through 60∘.
View SolutionA uniform L-shaped rod of mass 2m and length 2L, hangs from a hinge as shown (AO is horizontal and OB is vertical). If it is released from the position shown, then find the maximum angular velocity acquired by the end.
View Solution
