A uniform circular disc of radius R is placed on a frictionless horizontal plane. Another identical disc rotating with velocity ω0 is gently placed on top the first disc.The coefficient of friction between the discs is μ. The time in which both disc acquire same angular velocity is nRω0/8μg. Find the value of n.
The correct Answer is:3
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Matrix Matching Type Questions2videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)6videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
Similar Questions
A uniform circular disc of radius r placed on a rough horizontal plane has initial velocity v0 and angular ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
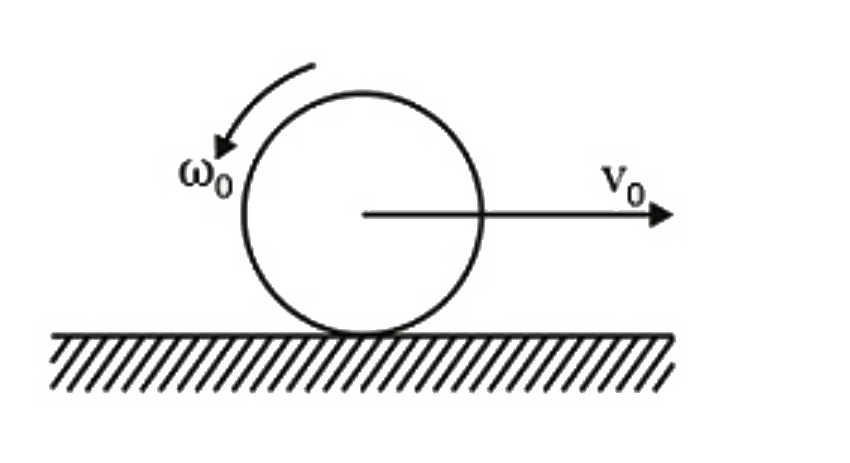 View Solution
View SolutionA uniform disc of radius r0 lies on a smooth horizontal plane. A similar disc spinning with the angular velocity ω0 is carefully lowered onto the first disc. How soon do both discs spin with the same angular-velocity if the friction coefficient between them is equal to μ?
View Solution
Knowledge Check
- Question 1 - Select One
A uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r - Question 2 - Select One
A uniform circular disc of radius R is rotating about its own axis with moment of inertia I at an angular velocity ω if a denser particle of mass m is gently attached to the rim of disc than its angular velocity is
AωBIω(I+mR)CI+mR2IωDIωI+mR2
A uniform disc of radius r0 lies on a smooth horizontal plane. A similar disc spinning with the angular velocity ω0 is carefully lowered onto the first disc. How soon do both discs spin with the same angular-velocity if the friction coefficient between them is equal to μ?
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 View Solution
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.View SolutionA coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View Solution

