A uniform disc of radius r0 lies on a smooth horizontal plane. A similar disc spinning with the angular velocity ω0 is carefully lowered onto the first disc. How soon do both discs spin with the same angular-velocity if the friction coefficient between them is equal to μ?
To solve the problem of how soon both discs spin with the same angular velocity after one is lowered onto the other, we can follow these steps:
Step 1: Understand the System
We have two uniform discs of radius r0. The first disc is at rest on a smooth horizontal plane, while the second disc is spinning with an angular velocity ω0. When the second disc is lowered onto the first, they will eventually reach a common angular velocity due to the friction between them.
Step 2: Apply Conservation of Angular Momentum
Before the second disc is placed on the first, the angular momentum of the system is solely from the second disc:
Linitial=I2ω0
where I2 is the moment of inertia of the spinning disc. The moment of inertia of a disc is given by:
I=12mr2
Thus, for the spinning disc,
I2=12mr20
So,
Linitial=12mr20ω0
After the second disc is placed on the first, both discs will rotate together with a common angular velocity ω. The total moment of inertia of the system is:
Ifinal=I1+I2=12mr20+12mr20=mr20
Thus, the final angular momentum is:
Lfinal=Ifinalω=mr20ω
By conservation of angular momentum:
Linitial=Lfinal
12mr20ω0=mr20ω
Step 3: Solve for Common Angular Velocity
Cancelling mr20 from both sides gives:
12ω0=ω
Thus, the common angular velocity when both discs start rotating together is:
ω=ω02
Step 4: Determine the Torque Due to Friction
The friction between the two discs will create a torque that changes their angular velocities. The frictional force f can be expressed as:
f=μN
where N is the normal force, which equals the weight of the upper disc mg (assuming m is the mass of the upper disc). Therefore, the frictional force is:
f=μmg
The torque τ due to this frictional force acting at a radius r0 is:
τ=f⋅r0=μmgr0
Step 5: Relate Torque to Angular Acceleration
The angular acceleration α can be found using:
τ=Iα
where I is the moment of inertia of the combined system:
I=mr20
Thus,
μmgr0=mr20α
Cancelling m from both sides gives:
μg=r0α⟹α=μgr0
Step 6: Use Kinematics to Find Time
Now, we can use the kinematic equation for angular motion:
ω=ω0+αt
For the upper disc:
ω02=ω0−αt
Substituting α:
ω02=ω0−μgr0t
Rearranging gives:
μgr0t=ω02
Thus,
t=ω0r02μg
Final Result
The time after which both discs will have the same angular velocity is:
t=ω0r02μg
We have two uniform discs of radius r0. The first disc is at rest on a smooth horizontal plane, while the second disc is spinning with an angular velocity ω0. When the second disc is lowered onto the first, they will eventually reach a common angular velocity due to the friction between them.
Before the second disc is placed on the first, the angular momentum of the system is solely from the second disc:
Linitial=I2ω0
where I2 is the moment of inertia of the spinning disc. The moment of inertia of a disc is given by:
I=12mr2
Thus, for the spinning disc,
I2=12mr20
So,
Linitial=12mr20ω0
Ifinal=I1+I2=12mr20+12mr20=mr20
Thus, the final angular momentum is:
Lfinal=Ifinalω=mr20ω
Linitial=Lfinal
12mr20ω0=mr20ω
Cancelling mr20 from both sides gives:
12ω0=ω
Thus, the common angular velocity when both discs start rotating together is:
ω=ω02
The friction between the two discs will create a torque that changes their angular velocities. The frictional force f can be expressed as:
f=μN
where N is the normal force, which equals the weight of the upper disc mg (assuming m is the mass of the upper disc). Therefore, the frictional force is:
f=μmg
τ=f⋅r0=μmgr0
The angular acceleration α can be found using:
τ=Iα
where I is the moment of inertia of the combined system:
I=mr20
Thus,
μmgr0=mr20α
Cancelling m from both sides gives:
μg=r0α⟹α=μgr0
Now, we can use the kinematic equation for angular motion:
ω=ω0+αt
For the upper disc:
ω02=ω0−αt
Substituting α:
ω02=ω0−μgr0t
Rearranging gives:
μgr0t=ω02
Thus,
t=ω0r02μg
The time after which both discs will have the same angular velocity is:
t=ω0r02μg
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example1videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.110videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples25videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform.
View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View Solutiona uniform circular disc of radiu8s r placed on a roughn horizontal plane has initial velocity v0 and an angul,ar velocity ω0 has shown The disc comes to rest after moving some distance in the direction of motion. Then
 View Solution
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 View Solution
View SolutionA uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, spectively. Find the
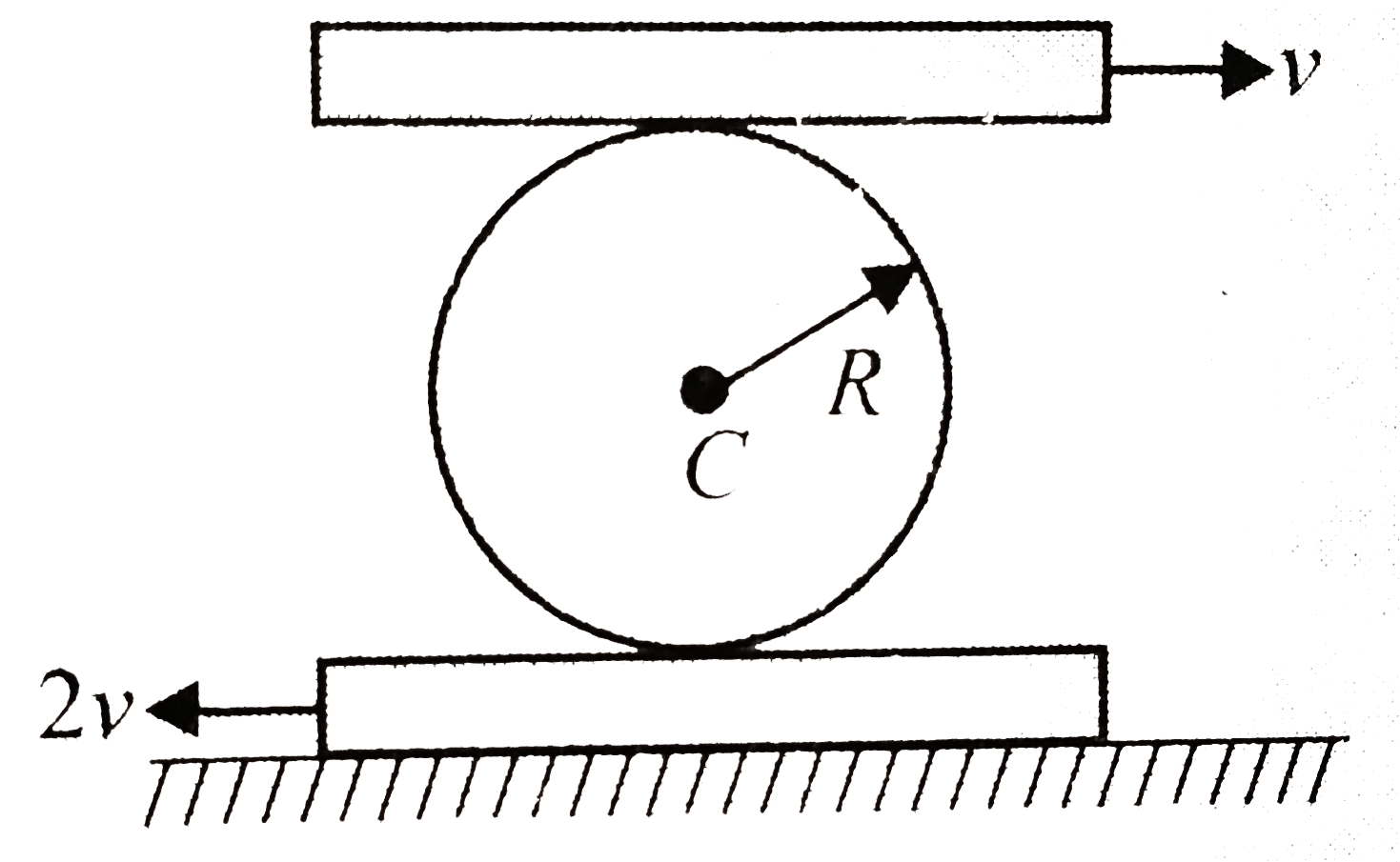
a. velocity of CM of the disc.
b. angular velocity of the disc.View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.View Solution
The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity ω0. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are
 View Solution
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is
 View Solution
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isView Solution

