A uniform string of length L and mass M is fixed at both ends while it is subject to a tension T . It can vibrated of frequencies (v) given by the formula (where n = 1 , 2, 3.....) Solution in Bengali
v=n2√TML
v=n2L√TML
v=12n√TML
v=n2√TML
Step by step video & image solution for A uniform string of length L and mass M is fixed at both ends while it is subject to a tension T . It can vibrated of frequencies (v) given by the formula (where n = 1 , 2, 3.....) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The magnetic field intensity at the centre of a cubical cage of identical wires of length 'a' due to a current I flowing as shown in the figure is
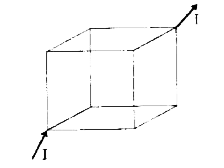
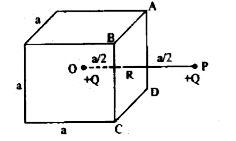
View SolutionConsider a region in free space bounded by the surfaces of an imaginary cube having sides of length a as shown in the diagram. A charge +Q is placed at the centre O of the cube. P is such a point outside the cube that the line OP perpendicularly intersects the surface ABCD at R and also OR=a/2. A charge +Q is placed at point P also. What is the total electric flux through the five faces of the cube other than ABCD?
View SolutionThe frequency (n) of vibration of a string is given as n = (1)/( 2 l) sqrt((T)/(m)) , where T is tension and l is the length of vibrating string , then the dimensional formula is
View SolutionThe frequency of vibration (v) of a string may depend upon length (I) of the string, tension (T) in the string and mass per unit length (m) of the string. Using the method of dimensions, derive the formula for v.
View SolutionA uniform string of length L and mass M is fixed at both end while it is subject to a tension T . It can vibrate at frequencies v given bby the formula (where, n=1,2,3,………..)
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionWhich of the following is not the law of a stretched string ? ( n , l , T and m are frequency of vibration , length of vibrating string , tension in string and linear mass density , respectively .)
View SolutionL लम्बाई तथा M द्रव्यमान की दोनों सिरों पर बंधी एकसमान डोरी में T तनाव है । इसके कम्पन की आवृत्ति का सूत्र है -
View SolutionA string of length 1m and mass 5g is fixed at both ends. The tension in the string is 12.5 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string (in m) is ______ .
View SolutionA string of mass per unit length "0.2 kg m"^(-1) and length 0.6 m is fixed at both ends such that it has a tension of 80 N. If the string is vibrating in its second overtone mode, then the frequency of the string is
View SolutionThe mass of string (M) = 2 . 5 g , length (l) = 25 cm and tension (T) = 25 N . Determine the fundamental frequency of transverse vibration in the string .
View SolutionA uniform string of length L and mass M is fixed at both ends while it is subject to a tension T . It can vibrated of frequencies (v) given by the formula (where n = 1 , 2, 3.....)
View SolutionThe frequency (n) of vibration of a string is given as n=(1)/(2l)sqrt(T/(m)), where T is tension and l is the length of vibrating string, then the dimensional formula for m is :
View SolutionA uniform string of length L and mass M is fixed at both ends while it is subject to a tension T. It can vibrate at frequencies (v) given by the formula where n= 1,2,3..........
View SolutionA uniform string of length L and mass M is fixed at both end while it is subject to a tension T. It can vibrate at frequencies v given bby the formula (where, n=1,2,3,………..)
View Solution
