A solid rectangular sheet has two different coefficients of linear expansion α1 and α2 along its length and breadth respectively. The coefficient of surface expansion is (for α1t<<1,α2t<<1)Solution in Bengali
α1+α22
2(α1+α2)
4α1α2α1+α2
α1+α2
Step by step video & image solution for A solid rectangular sheet has two different coefficients of linear expansion alpha_(1) " and " alpha_(2) along its length and breadth respectively. The coefficient of surface expansion is ("for " alpha_(1)t "<<"1, alpha_(2)t"<<"1) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
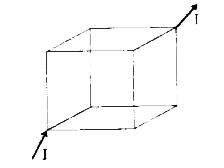
The magnetic field intensity at the centre of a cubical cage of identical wires of length 'a' due to a current I flowing as shown in the figure is
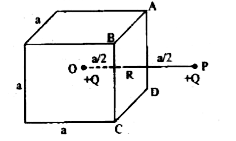
View SolutionConsider a region in free space bounded by the surfaces of an imaginary cube having sides of length a as shown in the diagram. A charge +Q is placed at the centre O of the cube. P is such a point outside the cube that the line OP perpendicularly intersects the surface ABCD at R and also OR=a/2. A charge +Q is placed at point P also. What is the total electric flux through the five faces of the cube other than ABCD?
View SolutionThe coefficient of linear expansion of crystal in one direction is alpha_(1) and that in every direction perpendicular to it is alpha_(2) . The coefficient of cubical expansion is
View SolutionThe ratio of coefficients of apparent expansions of the same liquid in two different vessels is 1:2 . If alpha_(1) and alpha_(2) are the coefficient of linear expansions then coefficient of real expansion of the liquid is
View SolutionIn an anisotropic medium the coefficients of linear expansion of a solid are α1, α2, and α3. In three mutually perpendicualr directions. Tjhe coefficient of volume expansion for the solid is
View SolutionTwo rods of length L1 and L2 are made of materials of coefficients of linear expansions α1 an α2 respectively such that L1α1=L2α2. The temperature of the rods is increased by ΔT and correspondingly the change in their respective lengths be ΔL1 and ΔL2
View Solution" The relation between coefficient of linear expansion "(alpha_(1))" and coefficient of volume expansion ( "alpha_(5)" ) is "
View SolutionTwo rods of different metals of coefficient of linear expansion α1 and α2 and initial length l1 and l2 respectively are heated to the same temperature. Find relation in α1,α2,l1 and l2such that difference between their lengths remain constant.
View SolutionTwo different wirese having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coeficient of linear expansion is :
View SolutionA solid rectangular sheet has two different coefficients of linear expansion alpha_(1) " and " alpha_(2) along its length and breadth respectively. The coefficient of surface expansion is ("for " alpha_(1)t "<<"1, alpha_(2)t"<<"1)
View SolutionShow that the coefficient of area expansion , (Delta A//A)//Delta T , of a rectangular sheet of the solid is twice its linear expansivity , alpha_(1) .
View SolutionShow that the coefficient of area expansion , (ΔA/A)/ΔT , of a rectangular sheet of the solid is twice its linear expansivity , α1.
View SolutionShow that the coefficient of area expansion , (Delta A//A)//Delta T , of a rectangular sheet of the solid is twice its linear expansivity , alpha_(1) .
View SolutionTwo different wires having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coefficient of linear expansion is :
View SolutionIf α1,α2andα3 are the coefficients of linear expansion of a solid along three mutually perpendicular directions, find the average coefficient of volume expansion of that material?
View SolutionThe coefficient of linear expansion of crystal in one direction is α1 and that in every direction perpendicular to it α2. The coefficient of cubical expansion is :
View Solution
