ABC is an equilateral triangle. X is point on AC, Prove that BX>XC and BX>AX.
Step by step video & image solution for ABC is an equilateral triangle. X is point on AC, Prove that BX > XC and BX > AX. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The base BC of a triangle ABC is bisected at the point (a, b) and equation to the sides AB and AC are respectively ax+by=1 and bx+ay=1 Equation of the median through A is:
View SolutionDelta ABC An equilateral triangle D, E is the points DE = 3 cm between AB and AC Delta ABC Perimeter.
View SolutionX is any point inside ΔABC, XA, XB and XC are joined 'E' is any point on AX. If EF∣∣AB,FG∣∣BC. Peove that EG∣∣AC.
View Solutionएक त्रिभुज ΔABC की भुजाओं AB,AC तथा BC की लंबाई क्रमशः 15 सेमी., 20 सेमी., 28 सेमी. है। भुजा BC पर बिंदु X इस प्रकार है कि AX, कोण ∠A को समद्विभाजित करता है -
(a) BX=….. (b) CX=……..
View Solutionआकृति में X तथा Y, ΔABC की समान भुजाओं AB और AC पर दो बिन्दु इस प्रकार है कि AX=AY तो सिद्ध करे कि XC=YB
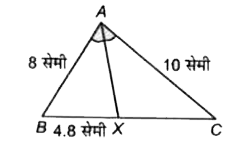
View Solutionचित्र में, ΔABC में रेखा AX,∠BAC का कोदरधहक है । रेखाखण्ड AB = 8 सेमी, AC = 10 सेमी तथा BX = 4.8 सेमी। रेखाखण्ड XC की माप होगी
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
View Solution
