Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Step by step video & image solution for Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If a rectangle and a parallelogram are equal in area and have the same base and are situated on the same side, then the ratio of perimeter of rectangle and that of parallelogram is k, then k is :
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn Fig.
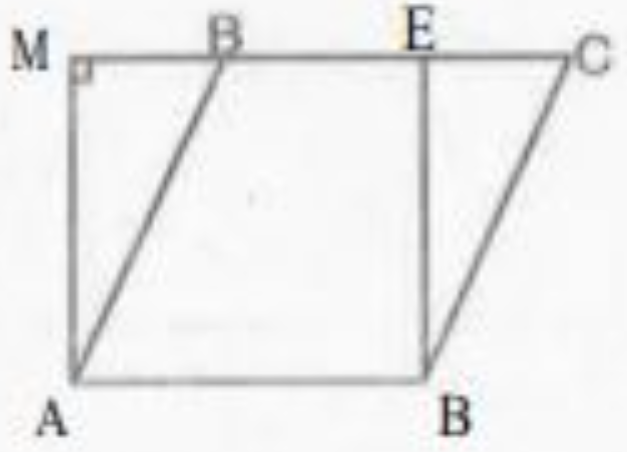 if parallelogram ABCD and rectangle ABEF are of equal area, then :
if parallelogram ABCD and rectangle ABEF are of equal area, then :
View SolutionIf perimeter of rectangle & Parallelogram is equal with same base. Find the ratio of area of rectangle and area of parallelogram.
View SolutionIf a rectangle and a parallelogram are equal in area and have the same base and are situated on the same side, then the ratio of perimeter of rectangle and that of parallelogram is k, then k is :
View SolutionIn Fig.

If parallelogram ABCD and rectangle ABEF are of equal area,
then :
View Solution
