From the top of a tower, the angles of depression of two objects on the same side of the tower are found to be α and β (α>β). If the distance between the objects is 'p' metres, show that the height 'h' of the tower is given by h=ptanαtanβtanα−tanβ
also determine the height of the tower, if p=50 m , α=60∘,β=30∘ Solution in Punjabi
Step by step video & image solution for From the top of a tower, the angles of depression of two objects on the same side of the tower are found to be alpha and beta (alpha >beta). If the distance between the objects is 'p' metres, show that the height 'h' of the tower is given by h=frac(p tan alpha tan beta)(tan alpha-tan beta) also determine the height of the tower, if p=50 m , alpha=60^@, beta=30^@ by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
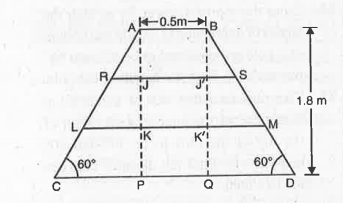
In the given figure, ABCD is a trapezium in which ABIICD. Line-segments RS and LM are drawn parallel to AB such that AJ = JK = KP. If AB = 0.5 m and AP = BQ = 1.8 m, find the length of AC, BD, RS and LM.
View SolutionUse Euclid's division algorithm to find HCF of : 36,84
View SolutionIn a city, the following weekly observations were made in a study of cost of living index for the year 1980-81.
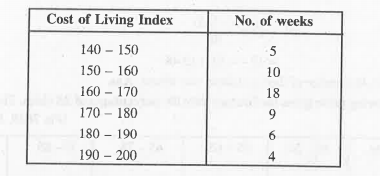 Calculate the mean weekly cost of living index by a suitable method.
Calculate the mean weekly cost of living index by a suitable method.
View SolutionA vertical tower sands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β .Prove that the height of the tower htanαtanβ−tanα
View SolutionA tower subtends an angle α at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b metres just above A is β . Prove that the height of the tower is btanαcotβ .
View Solutionएक झील से h मीटर ऊँचाई पर बादलों का उन्नयन कोण α है तथा झील में उसकी परछाई का अवनमन कोण β है। सिद्ध कीजिए की बादलों की ऊंचाई h(tanβ+tanα)tanβ−tanα है।
View Solutionएक मीनार के शीर्ष से मीनार की एक ही दिशा में स्थित दो वस्तुओं के अवनमन कोण α व β है (α>β) यदि इन वस्तुओं के बीच की दुरी p मीटर है तो सिद्ध कीजिए की मीनार की ऊंचाई|
h=ptanαtanβtanα−tanβ
View Solutionh मीटर ऊँचे भवन की चोटी और पाद से एक मीनार की चोटी का उन्नयन कोण क्रमशः α व β है|सिद्ध कीजिए की मीनार की ऊँचाई htanβtanβ−tanα है|
View SolutionFrom the bottom of a pole of height h the angle of elevation of the top of a tower is alpha and the pole subtends an angle beta at the top of the tower . Prove that the height of the tower is (h cot(alpha - beta))/(cot(alpha - beta) - cot alpha) .
View SolutionA tower subtends an angle α at a point A in the plane of its base and angle of depression of the foot of the tower at a point l metres just above A is β. Prove that the height of the tower is l tanαcotβ.
View Solutionh ऊंचाई की किसी मीनार की छोटी से दो वस्तुओ, जो मीनार के आधार वल रेखा में स्थित है के अवनमन कोण α और β(β>α) है दोनों वस्तुओ के बीच की दुरी ज्ञात कीजिएः
View Solutionपृथ्वी ताल पर किसी बिंदु से एक मीनार के शिखर का उनयन कोण α है और मीनार की और 'a' मीटर चलने पर उनयन कोण β हो जाता है। सिद्ध कीजिएः की मीनार की उचाई atanαtanβtanβ−tanα है
View SolutionAt a point on a level plane a vertical tower subtends an angle α and a pole of height a meters at the top of the tower subtends an angle β. Show that the height of the tower is a sinα cosec βcos(α+β).
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of the tower is α. The pole subtends an angle β at the top of the tower. Prove that the height of the tower is h sinα cosec βcos(α−β)
View SolutionFrom the top and bottom of a building of height h metres, the angles of elevation of the top of a tower are αandβ respectively. Then the height of the tower is :
View SolutionAngle of elevation of the top of a tower from a point on the ground beta is. Towards the root of the tower P Angle of elevation of the top of the tower when the meter goes forward alpha it happens. Prove that the height of the tower h=(Ptanalpha*tanbeta)/(tanalpha-tanbeta) Will happen If P=140m , beta=30^(@) And alpha=60^(@) If, then find the height of the tower.
View Solution
