A system of four masses m1,m2,m3,m4,two springs and a fixed pulley is shown in figure. The system is kept at rest by attaching the lower thread to a rigid peg . Determine the acceleration of all the masses after the lower thread has been cut . The springs are massless, pulley is frictionless and massless.
Clearly (m1+m2)>(m3+m4)
Let T1 be the tension in left spring and T2 that in right spring and T is tension in the string passing over the pulley.
Then for equilibrium of system
T1=m2g,T=(m1+m2)g ….(2)
and m3g+T2=T
From last equation
T2=T−m3g=(m1+m2−m3)g ....(3)
After the lower thread is cut off
Equationof motion of mass m1 is
m1g+T1−T=m2a3 ....(4)
Equation of motion of mass m2 is
m2g−T1=m2a2 ....(5)
Equation of motion mass m3 is
m3g+T2−T=m1a1 ....(6)
Equation of motion of mass m4 is
m4g−T2=m4a4 ....(7)
Using (1),(2) and (3) we get
a1=a2=a3=0
and a4=m4g−T2m4=(m4g−m1+m2−m3gm4=(m3+m4−m1−m2)gm4
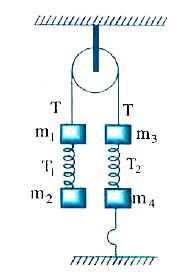
Similar Questions
Masses m1,m2,m3 and m4 are arranged in a system as shown in fig where m1+m2>m3+m4 The lower string keeping the system in equilibrium is burnt The masses start moving. Find the acceleration of masses if the threads are weightless and inextensible the springs are also weightless and the mass of the pulley is negligible.

View SolutionFour blocks and two springs are arranged as shown in fig. The system at rest, determine the accelration of all the loads immedialtely after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless, the mass of the pulley is negligible small, and there is no friction at the point of suspension.

View Solution
Knowledge Check
In the system shown in fig. m1>m2 . The system is held at rest by thread BC. Now thread BC is burnt. Answer the following:
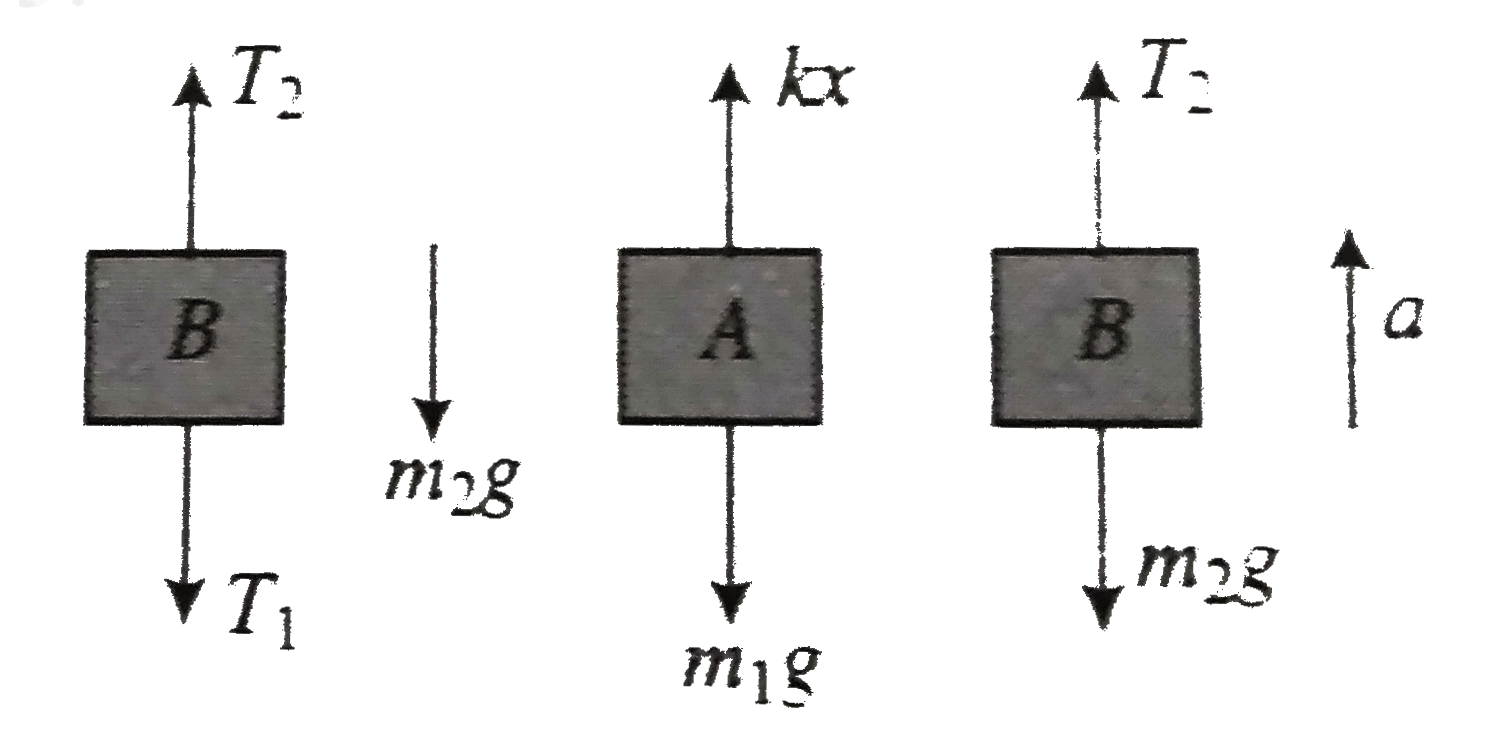
Just after burning the thread, what is the tension in the spring?Am1gBm2gCZeroDCannot saySystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 Ag/2 upwards, g downwardsBg upwards, g/2 downwardsCg upwards, 2g downwardsD2g upwards, g downwards
Ag/2 upwards, g downwardsBg upwards, g/2 downwardsCg upwards, 2g downwardsD2g upwards, g downwardsFind the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNone
System shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionIn the system shown in figure m1>m2. System is held at rest by thread BC. Just after the thread BC is burnt.

View SolutionIn the system shown in figure m1>m2. System is held at rest by thread BP. Just after the thread BP is burnt :
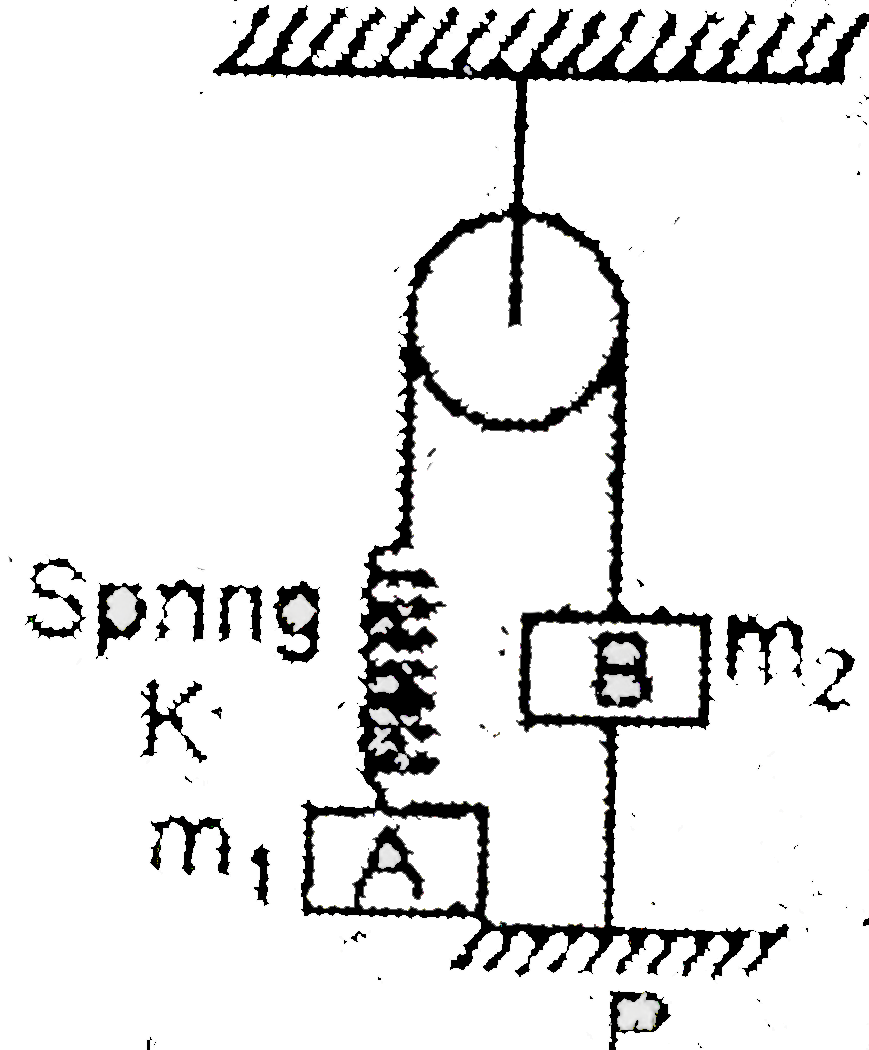
View SolutionIn the system shown in fig. m1>m2 . The system is held at rest by thread BC. Now thread BC is burnt. Answer the following:
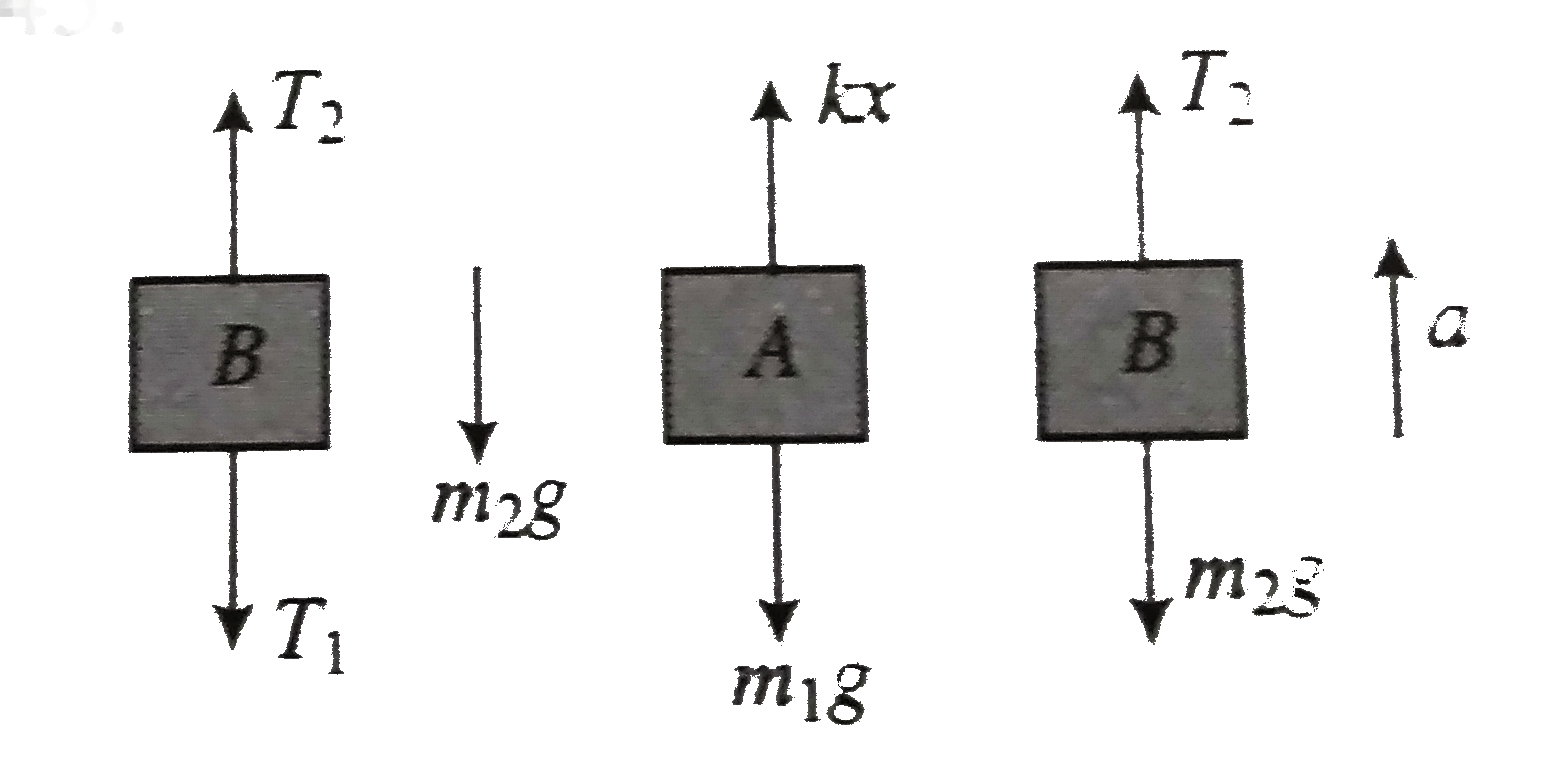
Just after burning the thread, what is the acceleration of m2?
View Solution
