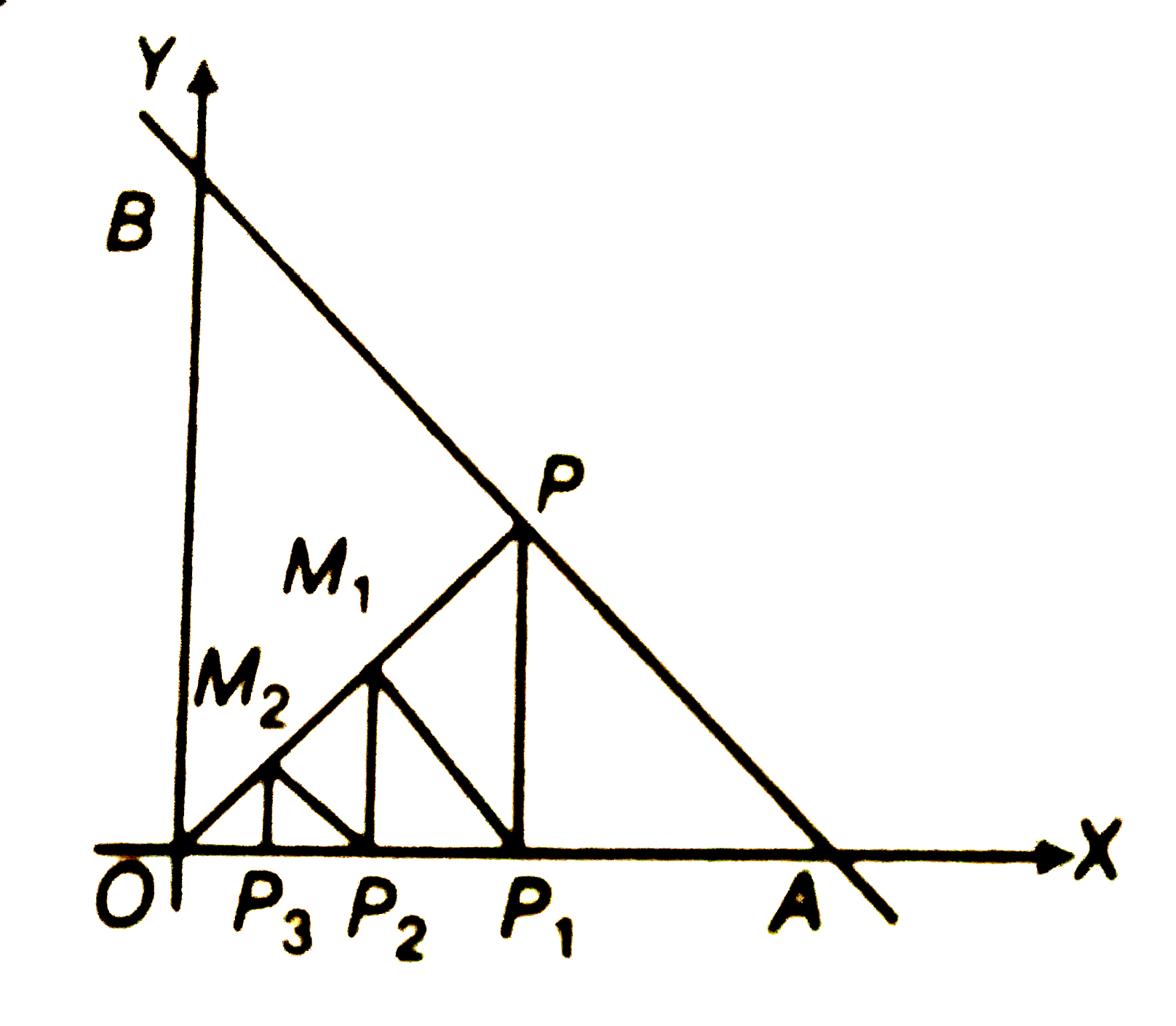
The line x+y=1 meets x-axis at A and y-axis at B,P is the midpoint of AB. P1 is the foot of the perpendicular from P to OA, M1 that form P1 to OP, P2 is that from M1 to OA and so on. If Pndenotes the nth foot of the perpendicualar on OA from Mn−1 then OPNSolution in Telugu
1/2
1/2n
1/2n/2
1/√2
The correct Answer is:B
Step by step video, text & image solution for The line x+y=1 meets x-axis at A and y-axis at B,P is the midpoint of AB. P_1 is the foot of the perpendicular from P to OA, M_1 that form P_1 " to OP, " P_2 is that from M_1 to OA and so on. If P_ndenotes the nth foot of the perpendicualar on OA from M_(n-1) " then " OP_N by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - PRACTICE SHEET (EXERCISE-IV Problems on Angle between lines, Foot, Image, Orthocentre, Circumcentre, Incentre, Angle Bisector and Locus) (LEVEL-II More than One correct answer Type Questions)
3 Videos
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - PRACTICE SHEET (EXERCISE-IV Problems on Angle between lines, Foot, Image, Orthocentre, Circumcentre, Incentre, Angle Bisector and Locus) (LEVEL-II Linked Comprehension Type Questions)
6 Videos
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - PRACTICE SHEET (EXERCISE-III Problems on point of intersection of lines and concurrency of lines) (LEVEL- II Integer Type Questions)
1 Videos
- REVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - PROPERTIES OF TRIANGLES
57 Videos
- TANGENT AND NORMAL BOOK - AAKASH SERIESCHAPTER - TANGENT AND NORMAL EXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
48 Videos
Similar Questions
If (xy) is a variable point on the line y=2x lying between the line 2(x+1)+y=0 and x+3(y-1)-0, then
View SolutionA (1,3) and C (-2/5,-2/5) are the vertices of a triangle ABC and the equation of the internal angle bisector of ∠ABCisx+y=2
Equation of BC is
View SolutionFor all real values of a and b, line(2a+b)x+(a+3b)y+(b−3a)=0andmx+2y+6=0 are concurrent. The |m| is equal to
View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)
View SolutionTwo points A and B move on the positive direction of x-axis and y-axis respectively, such that OA + OB K. Show that the locus of the foot of the perpendicular from the origin O on the line ABís (x + y)(x2 + y2) = Kxy. · (0,b)B Let the equation of AB be =1 a
View SolutionThe line x+ y = 1 meets X-axis at A and Y-axis at B,P is the mid-point of AB, P_1 is the foot ofperpendicular from P to OA, M_1, is that of P_1, from OP;P_2, is that of M_1 from OA, M_2, is that of P_2, from OP; P_3 is that of M_2, from OA and so on. If P_n denotes the nth foot of the perpendicular on OA, then find OP_n.
View SolutionA line is drawn from a point P(x,y) on the curve y=f(x), making an angle with the x-axis which is supplementary to the one made by the tangent to the curve at P(x,y). The line meets the x-axis at A. Another line perpendicular to it drawn from P(x,y) meeting the y-axis at B. If OA=OB, where O is the origin, the equation of all curves which pass through (1,1) is
View SolutionThe line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot of perpendicular from P to OA,M1 is that of P1 from OP,P2 is that of M1 from OA,M2 is that of P2 from OP,P3 is that of M2 from OA and so on. If Pn denotes theb nth foot of the perpendicular on OA, then find OPn
 .
.
View SolutionOA is the chord of the parabola y2=4x and perpendicular to OA which cuts the axis of the parabola at C. If the foot of A on the axis of the parabola is D, then the length CD is equal to
View SolutionIf P1,P2,P3,………,Pn are n points on the line y = x all lying in the first quadrant, such that (OPn)=n(OPn−1) (O is origin ) , OP1= and Pn=(2520√2,2520√2), then n =
View SolutionAandB are two variable points on xandy axes such that OA+OB=1/2. Then the locus of the foot of the perpendicular from the origin on the line AB is
View SolutionThe line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot ofperpendicular from P to OA,M1, is that of P1, from OP;P2, is that of M1 from OA,M2, is that of P2, from OP;P3 is that of M2, from OA and so on. If Pn denotes the nth foot of the perpendicular on OA, then find OPn.
View SolutionP1,P2 are points on either of the two lines y−√3|x|=2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1,P2 on the bisector of the angle between the given lines.
Thinking Process : Here, equation y−√3|x|=2 represents two different lines for x>0andx<0 and they are bisector of Y -axis. P1andP2 are points at a distance 5 unit from point of intersection. The y coordinate of the foot of perpendicular on Y-axis is 2+5cos(30∘).
View SolutionTwo points A and B move respectively on the positive x-axis and y-axis in such a way that OA + OB = K. Show that the line foot of the perpendicular from the original point O to the line AB (x+y)(x^(2) + y^(2)) = Kxy Will happen.
View Solution
