If A=(-2, 3, 4), B= ( 1, 2, 3) are two points and P is the point of intersection of AB and zx-plane, then Px+Py+Pz= Solution in Telugu
6
−8
8
0
The correct Answer is:c
Step by step video & text solution for If A=(-2, 3, 4), B= ( 1, 2, 3) are two points and P is the point of intersection of AB and zx-plane, then P_(x)+P_(y)+P_(z)= by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTRUE SHEET (ADVANCED)) (More than One correct answer Type Questions)
6 Videos
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTRUE SHEET (ADVANCED)) (Matrix Matching Type Questions)
1 Videos
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - PRACTICE SHEET (EXERCISE-I) (LEVEL-II) (Integer Type Questions)
1 Videos
- 2D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 2D-COORDINATE SYSTEMEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
14 Videos
- 3D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D-COORDINATE SYSTEMEXERCISE - PRACTICE EXERCISE
40 Videos
Similar Questions
P(1, 1, 1) and Q(1, 1, 1) are two points in the space such that PQ=√27, the value of l can be
View SolutionThe point to which the axes should be translated to eliminate first degree terms in the equation 2x2−2y2+z2−4x+8y−5=0 is
View SolutionIf the controid of the tetrahedron OABC where A,B,C are the points (a,2,3), (1,b,2) and (2,1,c) be (1,2,3) and the point (a,b,c) is at distance 5√λ from origin, then λ2 must be equal to.
View SolutionFind the area of equitateral triangle formed by (a,1), (1,b), (0,0) where o<a,b<1
View SolutionThe point (-1,4,-2) lie in the octant
View SolutionLet P1=x+y+z+1=0,P2=x−y+2z+1=0,P3=3x+y+4z+7=0 be three planes. Find the distance of line of intersection of planes P1=0 and P2=0 from the plane P3=0.
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
View Solutionमान लीजिए P1:2x−y+z=2
तथा P2∵x+2y−z=3 दो समतल है |
समतल P1 तथा P2 के प्रतिच्छेद बिंदु तथा बिंदु (3,2,1) से होकर जाने वाला समतल होगा
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View Solutionमान लीजिए कि R3 में P1:y=0 और P2:x+z=1 दो समतल है। माना कि P3 एक समतल है जो समतल P1 और P2 से भिन्न है तथा P1 एवं P2 के प्रतिच्छेदन से जाता हैं यदि बिंदु (0,1,0) से P3 की दूरी 1 है। तथा बिंदु (α,β,γ) से P3 की दूरी 2 है तब निम्नलिखित संबंध (संबंधों) में कौन सा (से) संतुष्ट होते है?
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View Solutionमान लीजिए कि R3 में P1:y=0 और P2:x+z=1 दो समतल है। माना कि P3 एक समतल है जो समतल P1 और P2 से भिन्न है तथा P1 एवं P2 के प्रतिच्छेदन से जाता हैं यदि बिंदु (0,1,0) से P3 की दूरी 1 है। तथा बिंदु (α,β,γ) से P3 की दूरी 2 है तब निम्नलिखित संबंध (संबंधों) में कौन सा (से) संतुष्ट होते है?
View Solutionमाना तीन समतल है :
P1=2x+y+z=1
P2=x−y+z=2
P3=ax−y+3z=5
तीनों समतल एक दूसरे को XOY समतल में बिन्दुP पर तथा YOZ समतल में बिन्दु Q पर प्रतिच्छेद करते है। मूलबिन्दु है।
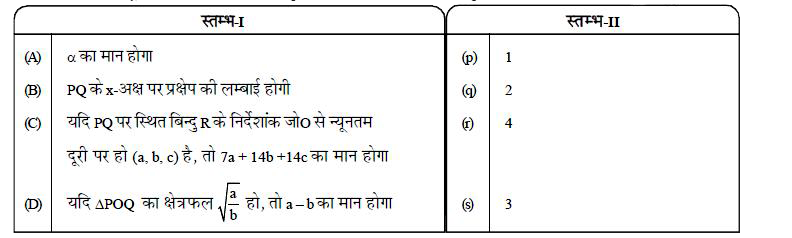
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View Solution
