If A is any square matrix. Observe the following lists and matching from List - I to List - II is
List-IList-II(A)A2=A(1) Orthogonal matrix(B)A2=I(2) Symmetric matrix(C)A2=0(3) Idempotent matrix(D)A.AT=ATA=I(4) Nilpotent matrix(5) Involutory matrix
A
ABCD2541
B
ABCD3241
C
ABCD3541
D
ABCD3542
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - ALGEBRA OF MATRICES -PRACTICE EXERCISE
41 Videos
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - DETERMINANTS- EXERCISE - I
15 Videos
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - ALGEBRA OF MATRICES -EXERCISE - I
47 Videos
- MATHEMATICAL INDUCTIONBOOK - AAKASH SERIESCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - PRACTICE SHEET (EXERCISE-I) LEVEL-I (Principle of Mathematical Induction) (Straight Objective Type Questions)
55 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
Similar Questions
Knowledge Check
If B is an idempotent matrix, and A=I−B, then
AA2=ABA2=ICAB=ODBA=OIf a square matrix A is such that ∀T=I=ATA, then|A| is equal to
A0B±1C±2DNone of the above
Matrix-Matching problems:
[A] Match the List-I with List-II:
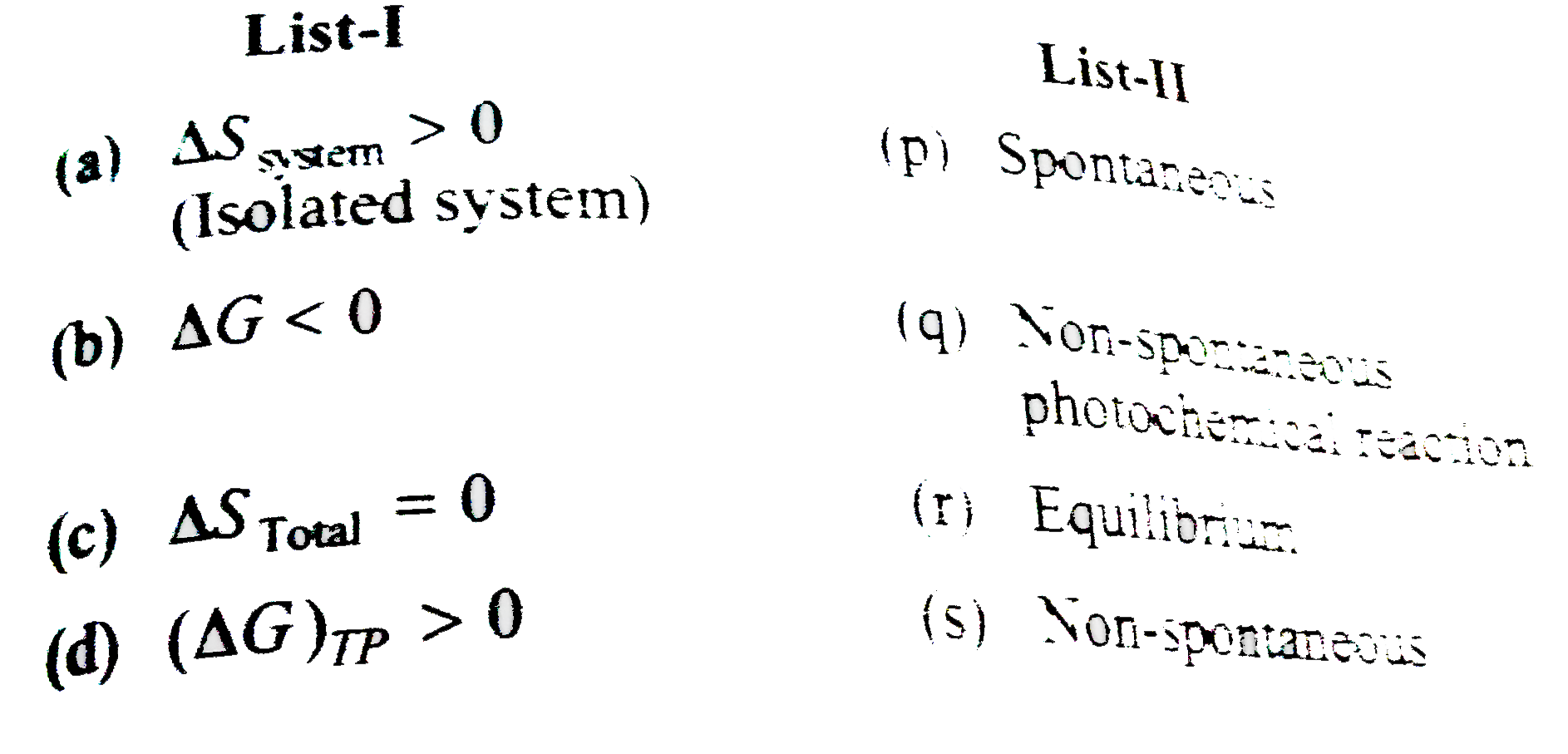
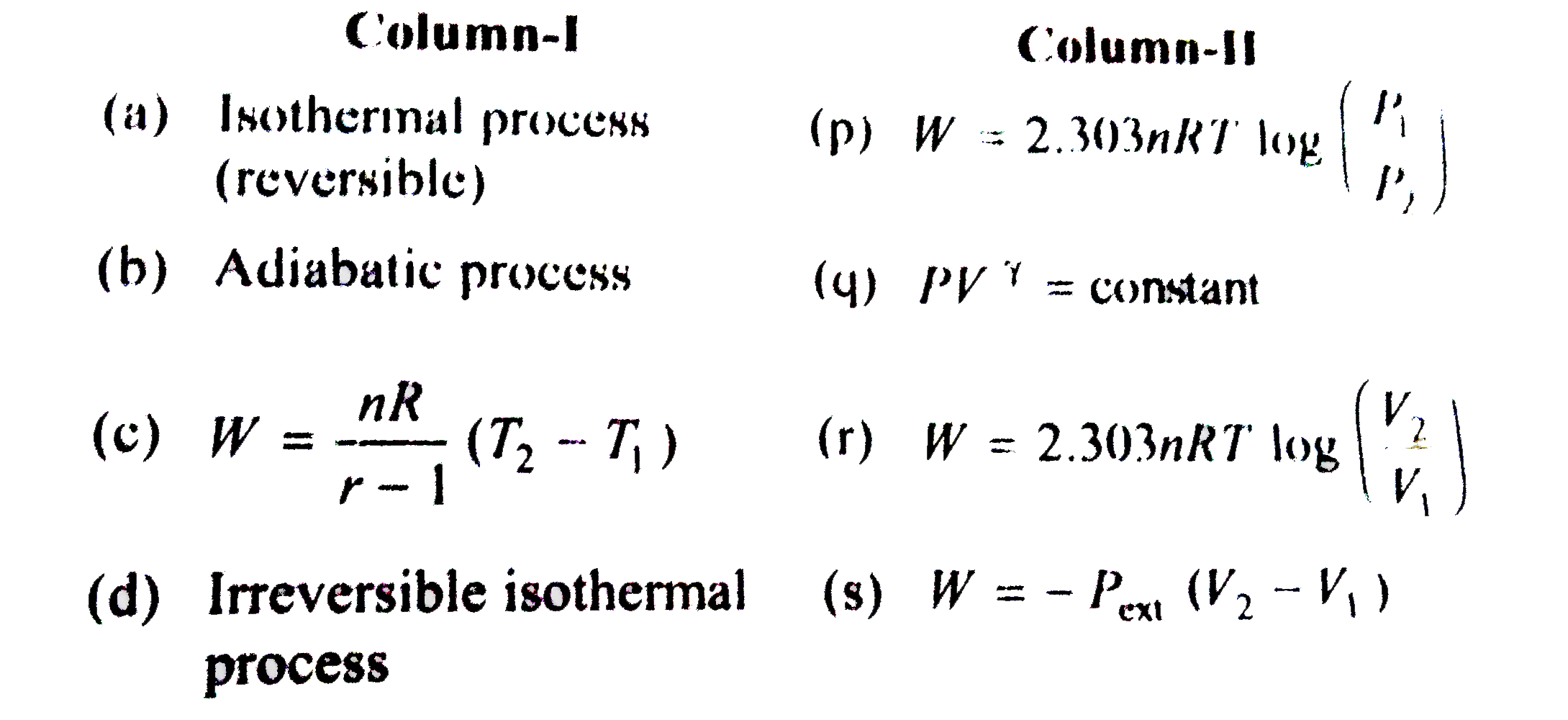
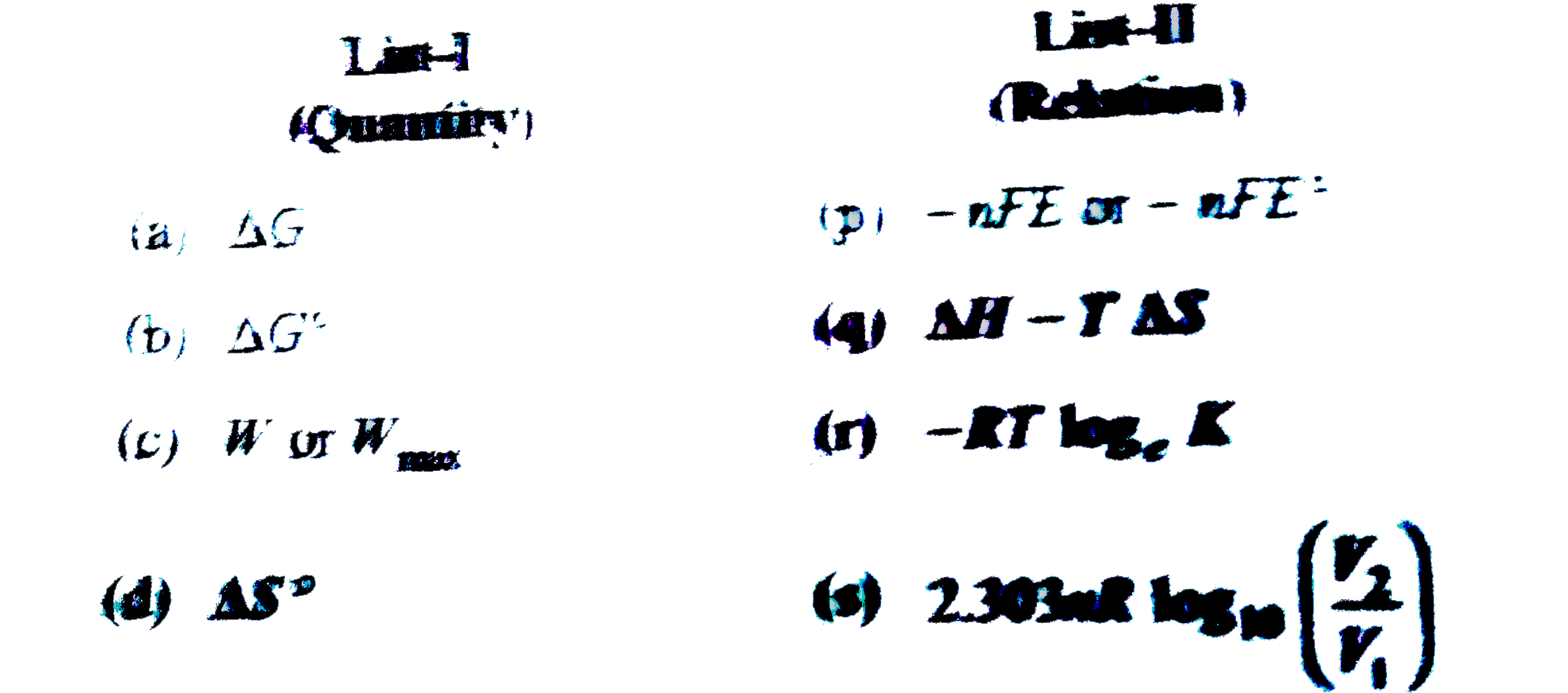
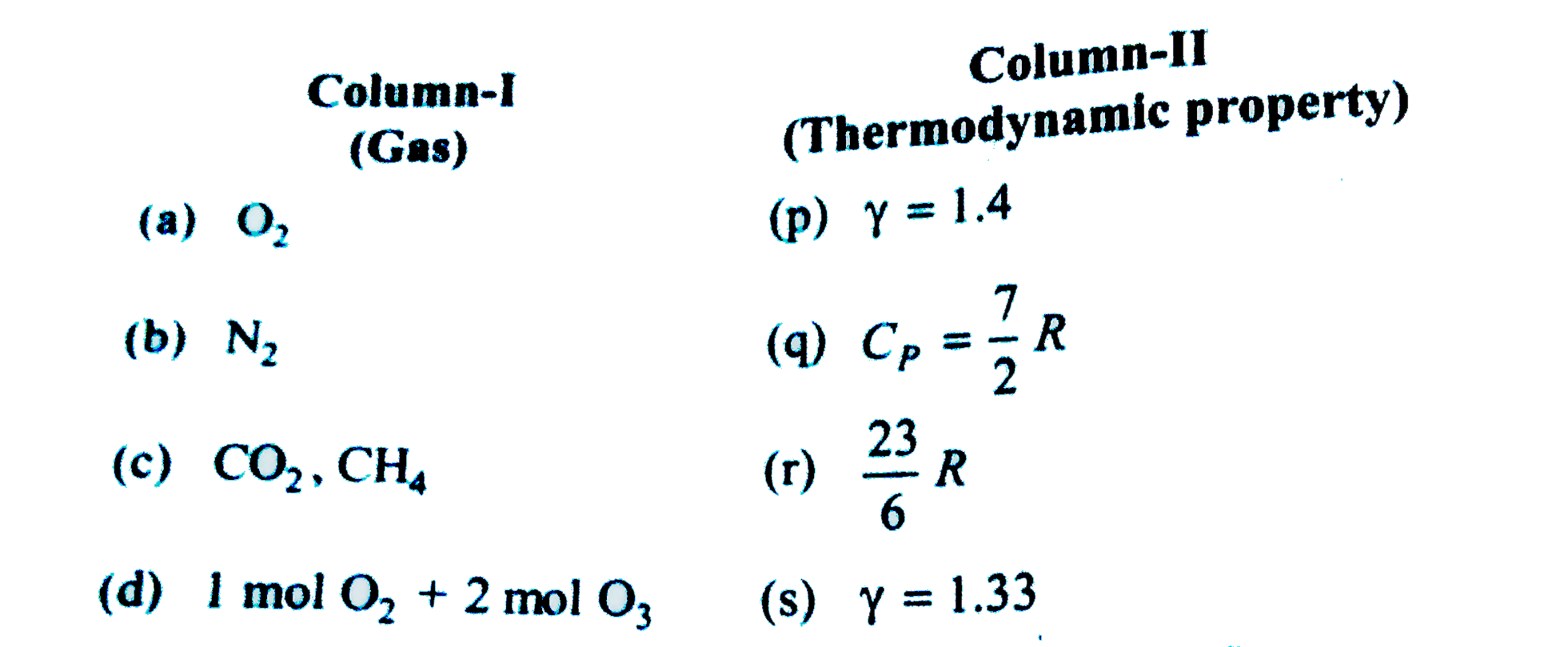
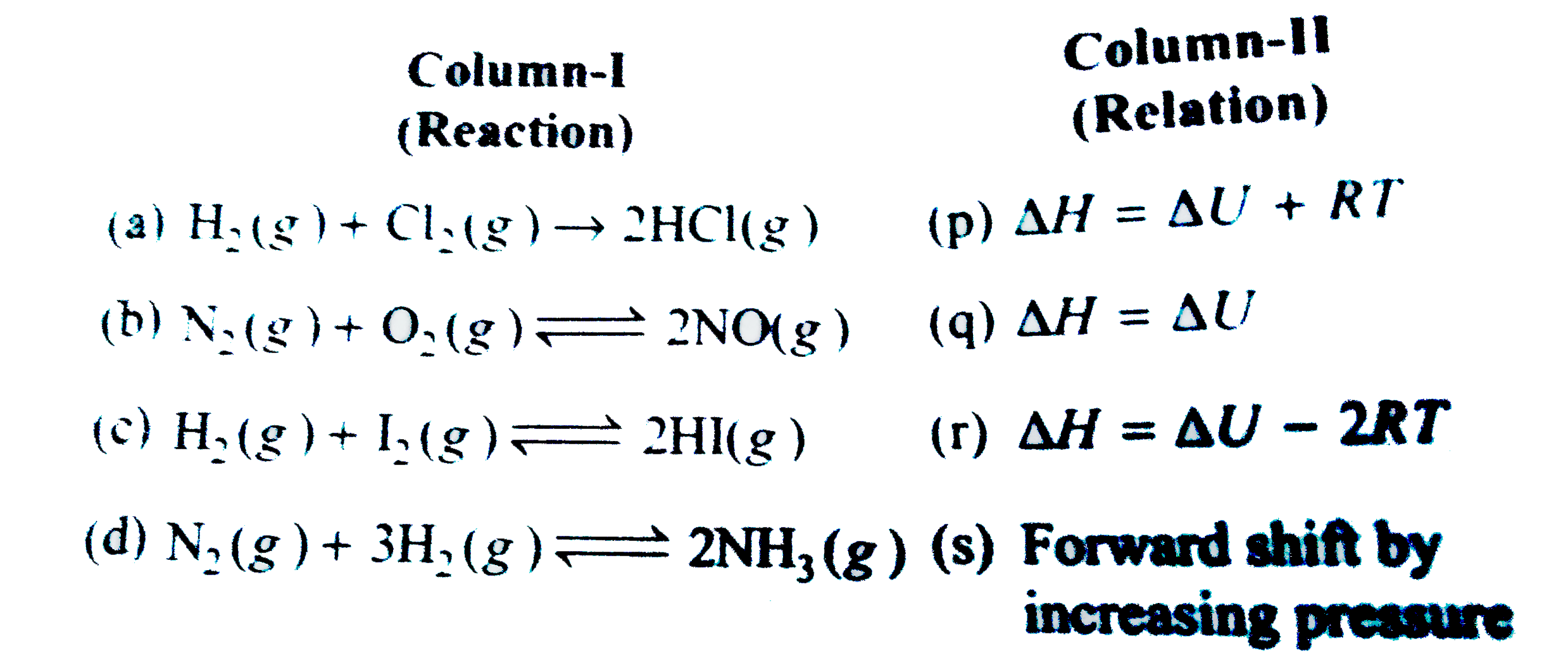
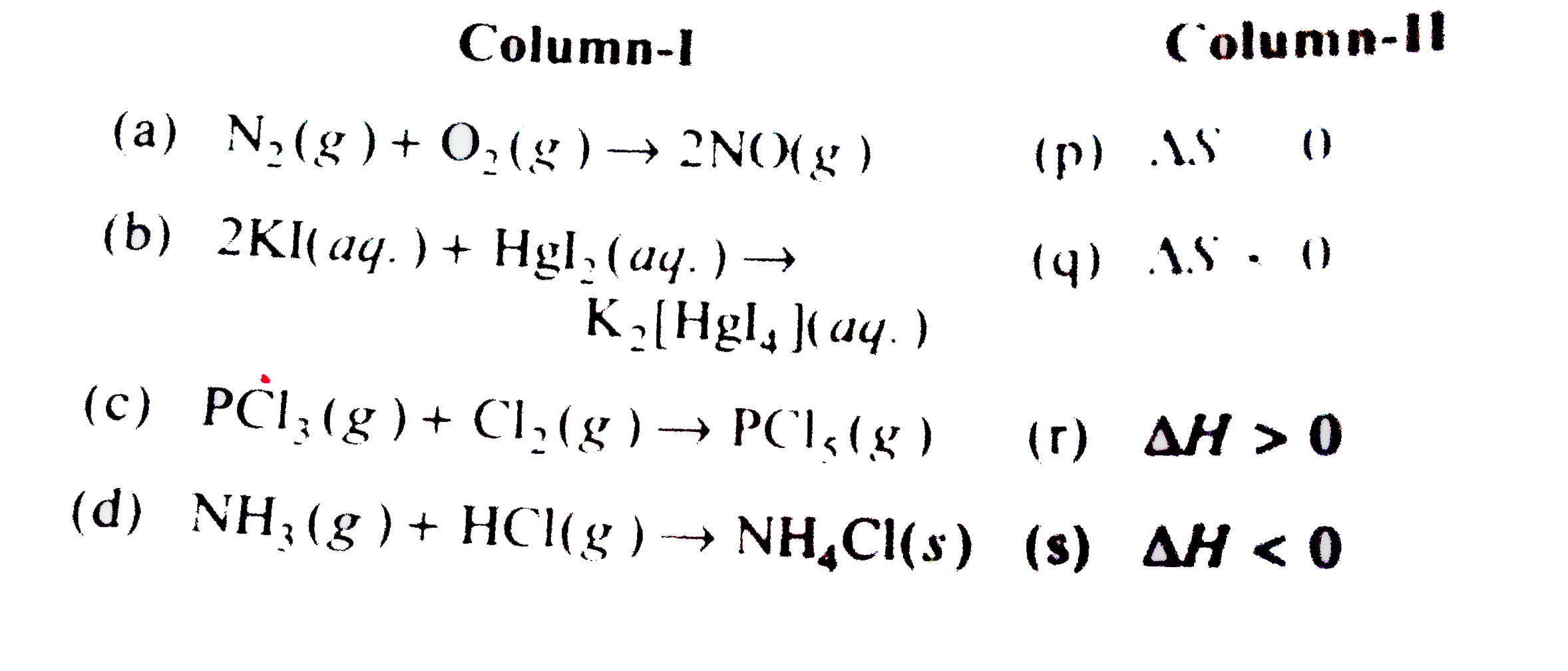
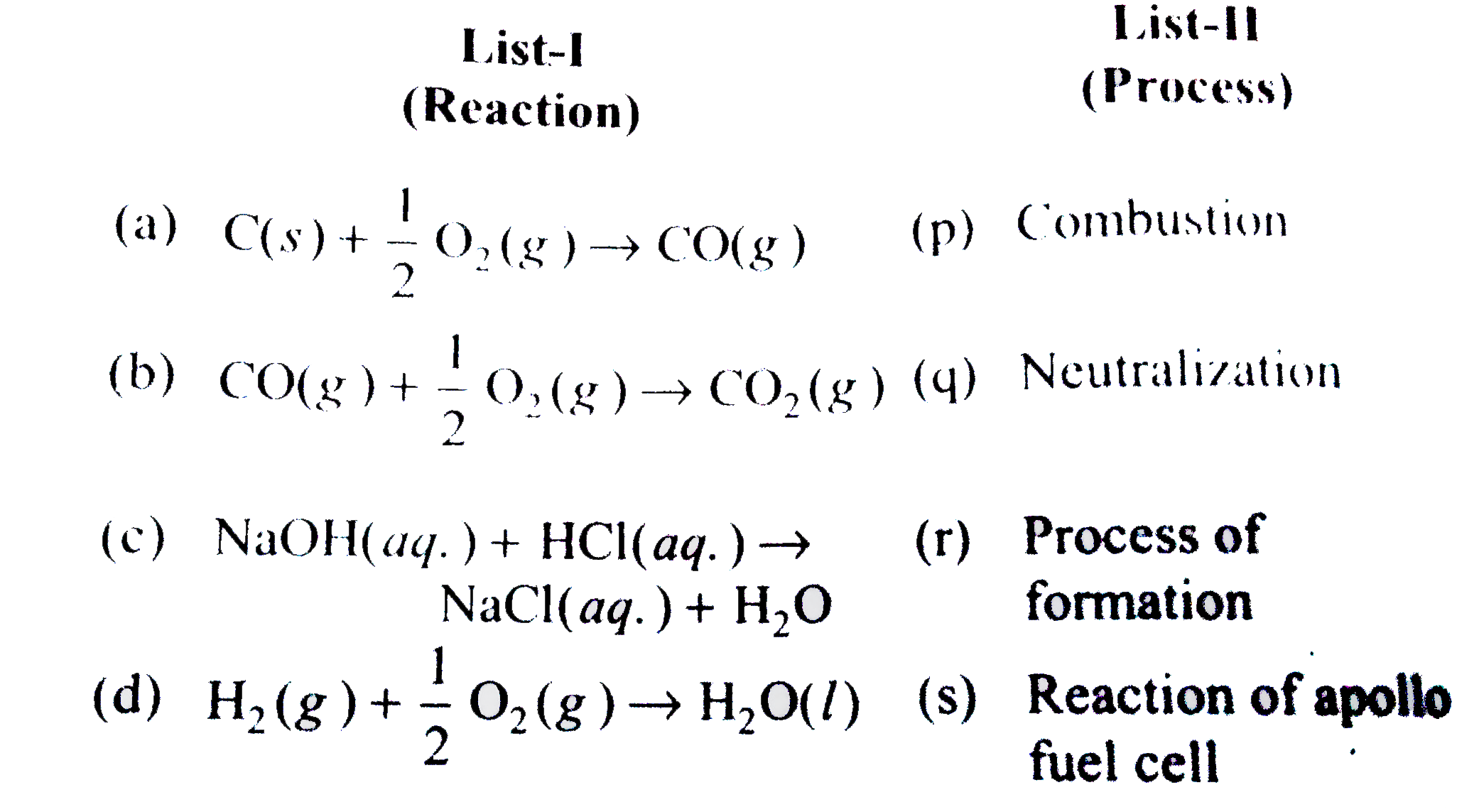
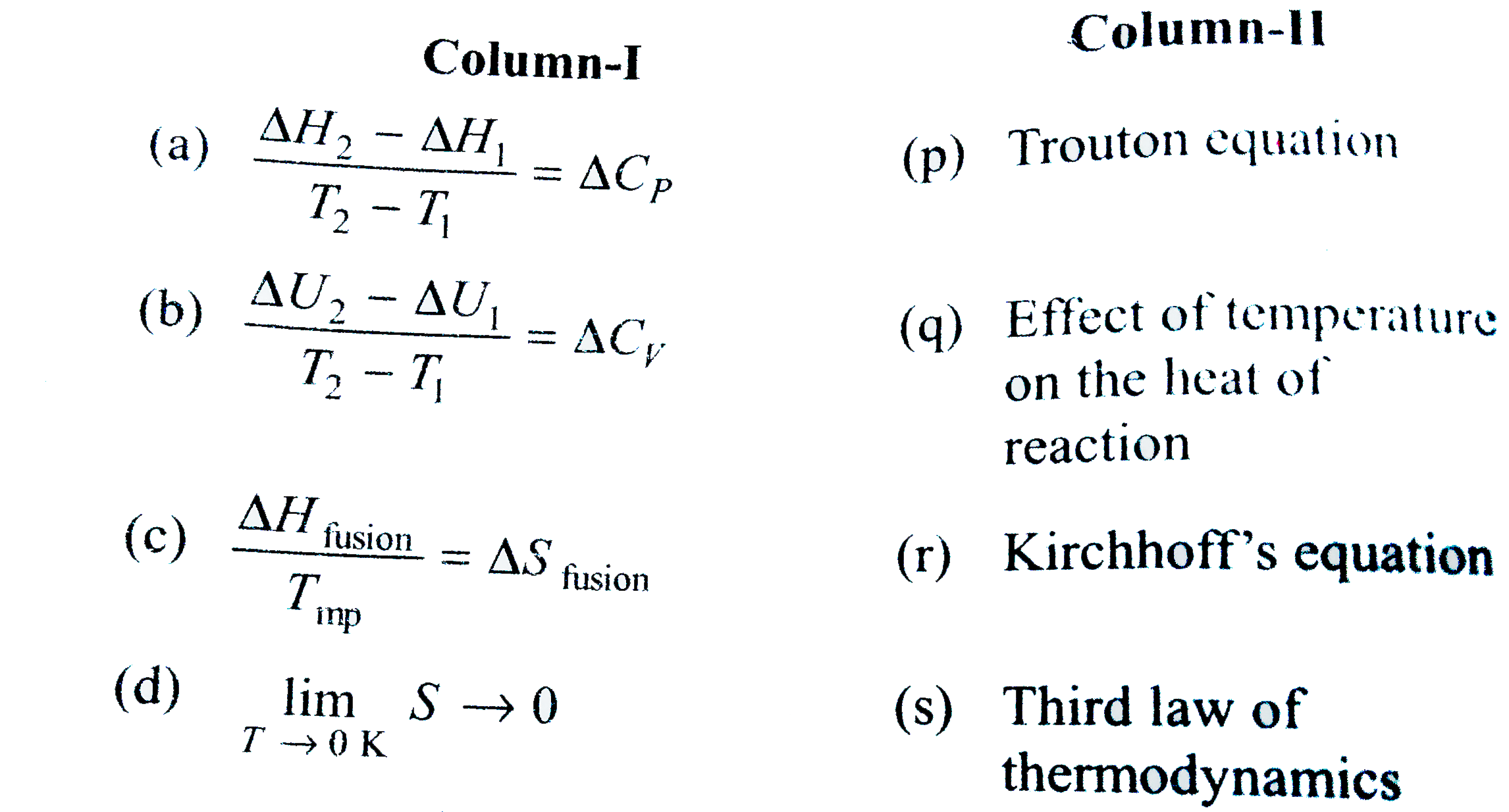
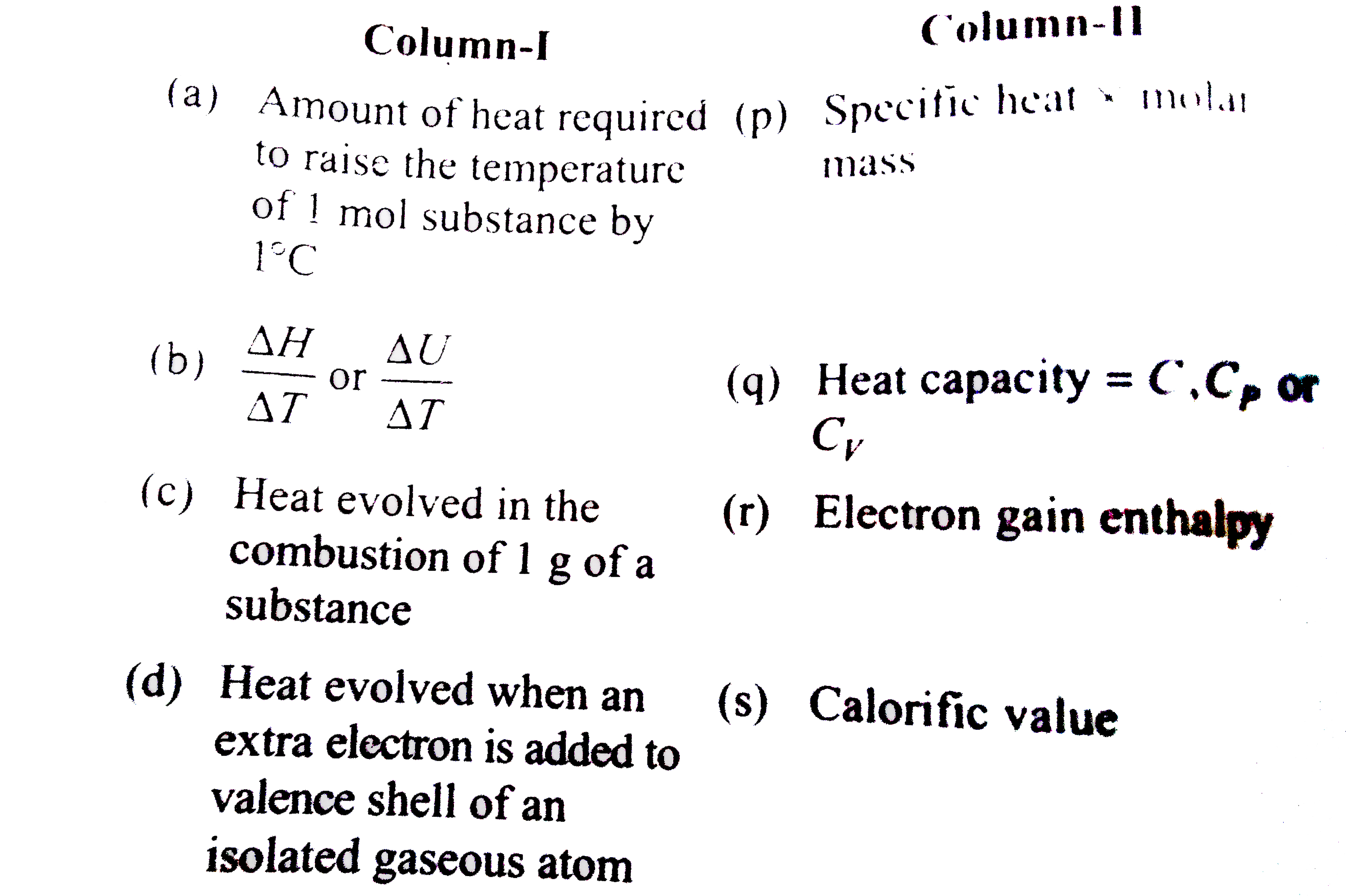
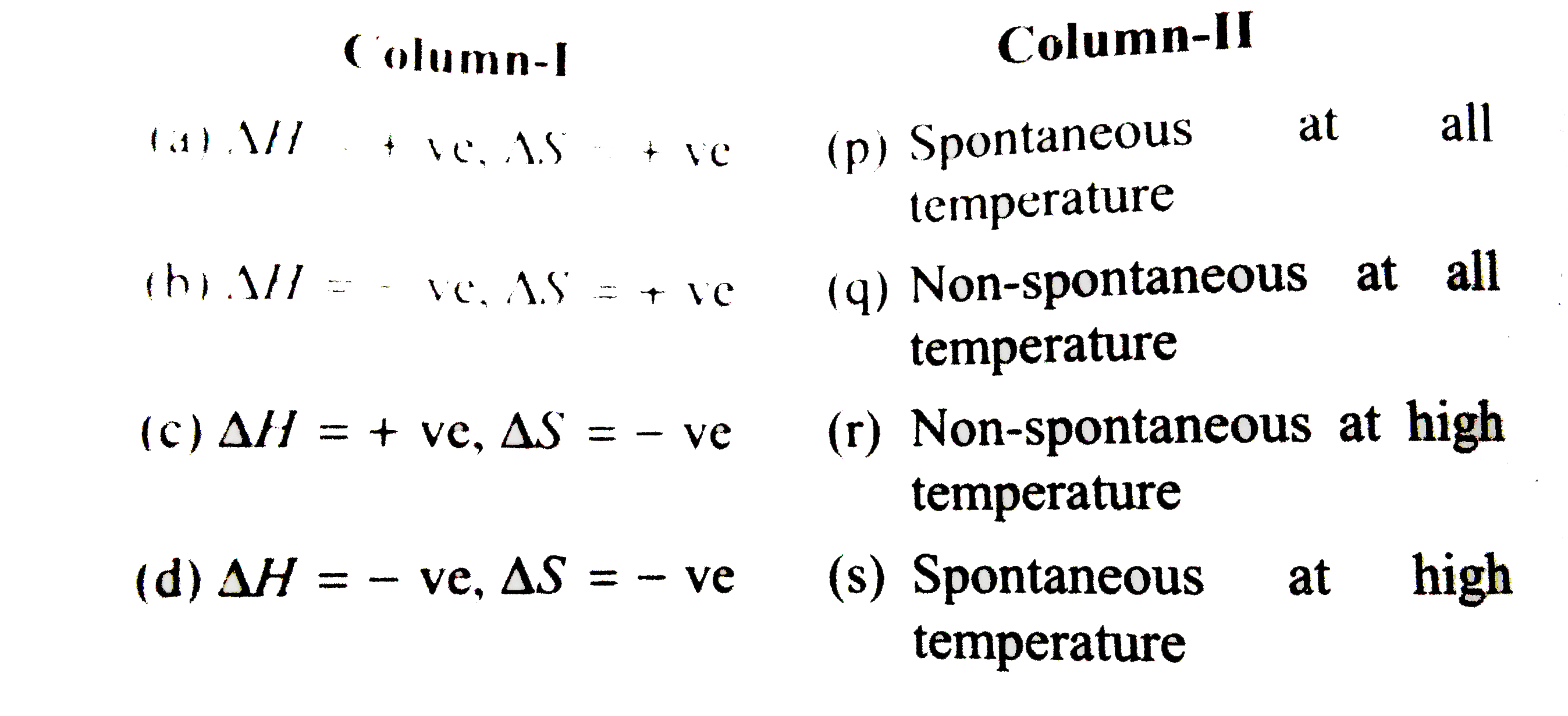
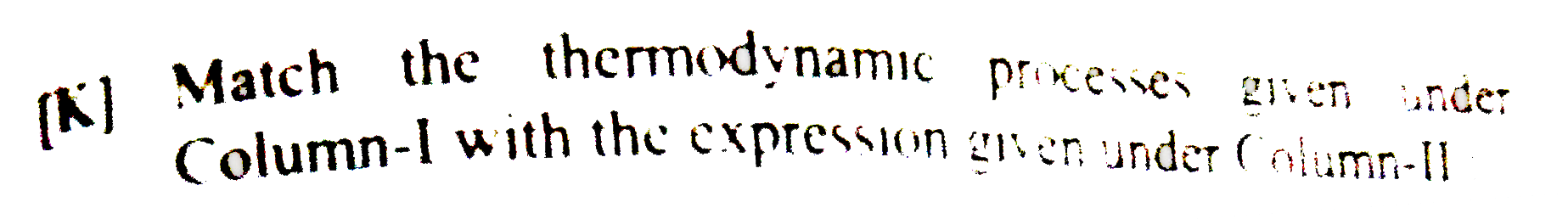

View SolutionMatch List - I with List - II.
List-IList-II(a)Torque(i)MLT−1(b)Impulse(ii)MT−2(c )Tension(iii)ML2T−2(d)Surface Tenion(iv)MLT−2
View SolutionIf A is any square matrix such that A+I2 and A−I2 are orthogonal matrices, then
View SolutionThe matrix A=⎡⎢⎣−5−8035012−1⎤⎥⎦ is (A) idempotent matrix (B) involutory matrix (C) nilpotent matrix (D) none of these
View SolutionThe matrix A=⎡⎢⎣−5−8035012−1⎤⎥⎦ is (A) idempotent matrix (B) involutory matrix (C) nilpotent matrix (D) none of these
View SolutionIf A^2 = I, then matrix A is Orthogonal matrix Idempotent matrix Involutory matrix Nilpotent matrix
View Solution
