Observe the following lists and matching from List - I to List - II is
Solution in Telugu
The correct Answer is:B
Step by step video, text & image solution for Observe the following lists and matching from List - I to List - II is {:("List-I","List-II"),((A)[(0,1),(1,0)],"(1) skew symmetric matrix"),((B)[(2,-5),(-5,2)],"(2) Symmetric matrix"),((S)[(0,x),(-x,0)],"(3) Hermitian matrix "),((D)[(1,2+3i),(2-3i,5)],"(4) Involutory matrix"),(,"(5) Idempotent matrix"):} by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - DETERMINANTS- EXERCISE - I
15 Videos
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - DETERMINANTS- EXERCISE - II
52 Videos
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - ALGEBRA OF MATRICES - EXERCISE - II
34 Videos
- MATHEMATICAL INDUCTIONBOOK - AAKASH SERIESCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - PRACTICE SHEET (EXERCISE-I) LEVEL-I (Principle of Mathematical Induction) (Straight Objective Type Questions)
55 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
Similar Questions
Elements of ⎡⎢⎣1−100423−46⎤⎥⎦ with their cofactors and choose the correct answer
Element Co factor(I) −1(a) −2(II) 1(b) 32(III) 3(c) 4(IV) 6(d) 6(e) −6
View SolutionIf A=[1321] then the determinant of A2−2A is
View SolutionIf A=⎡⎢⎣a2abacabb2bcacbcc2⎤⎥⎦ and a2+b2+c2=1, then A2=
View SolutionLet P(n) denote the statement that n2+n is odd. It is seen that P(n)⇒P(n+1),P(n) is true for all
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionFor the matrix A=[1567], verify that.
(i) (A+A′)is a symmetric matrix
(ii) (A−A′)is a skew symmetric matrix
View SolutionThe matrix A=⎡⎢⎣−5−8035012−1⎤⎥⎦ is (A) idempotent matrix (B) involutory matrix (C) nilpotent matrix (D) none of these
View SolutionThe matrix A=⎡⎢⎣0−585012−8−120⎤⎥⎦ is a (a) diagonal matrix (b) symmetric matrix (c) skew-symmetric matrix (d) scalar matrix
View SolutionMatrix-Matching problems:
[A] Match the List-I with List-II:
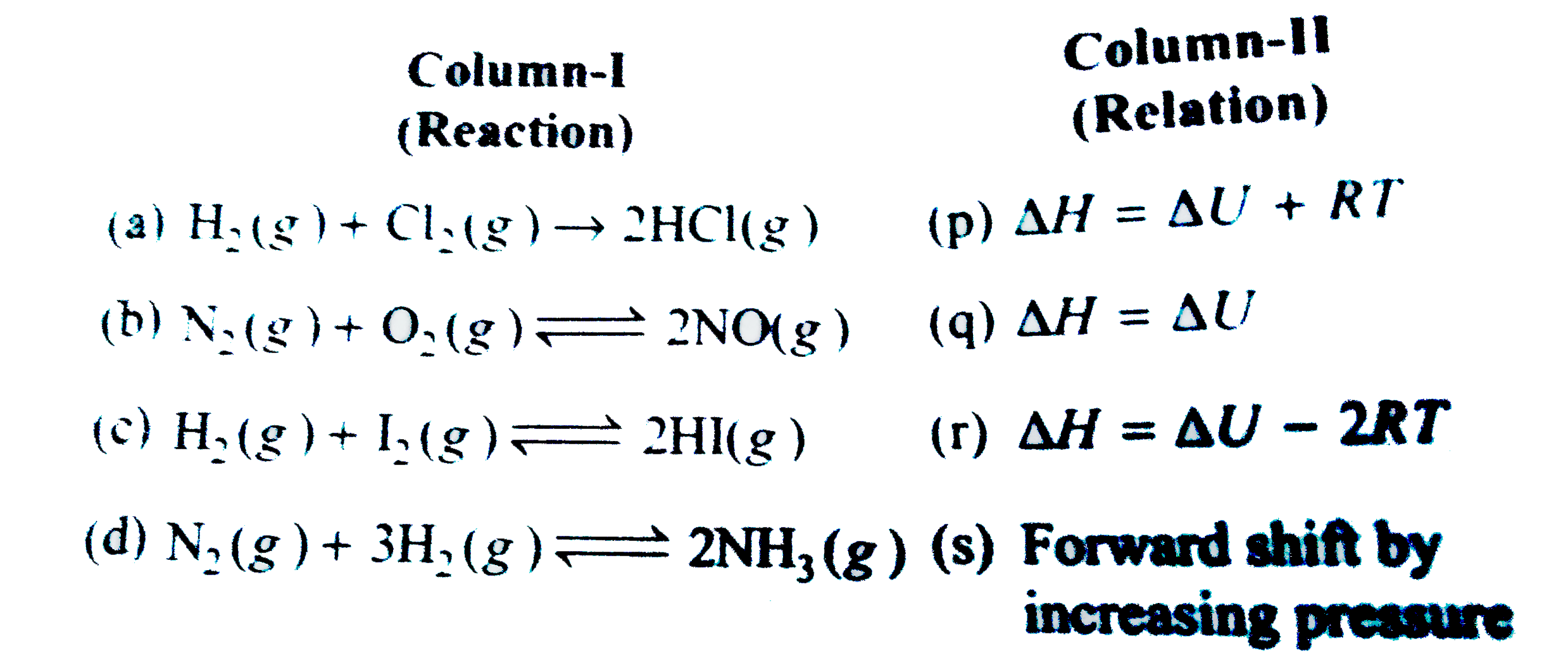
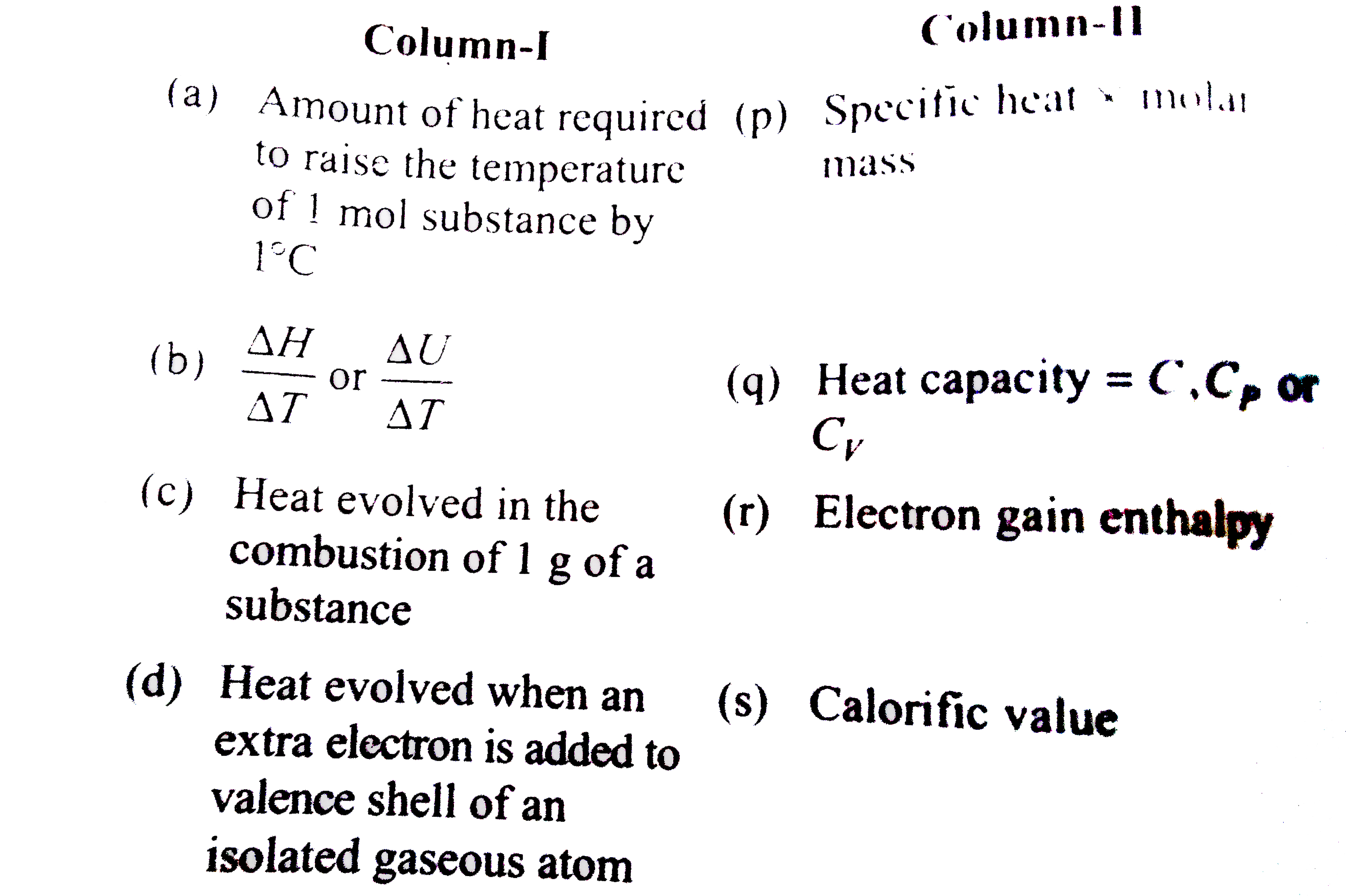
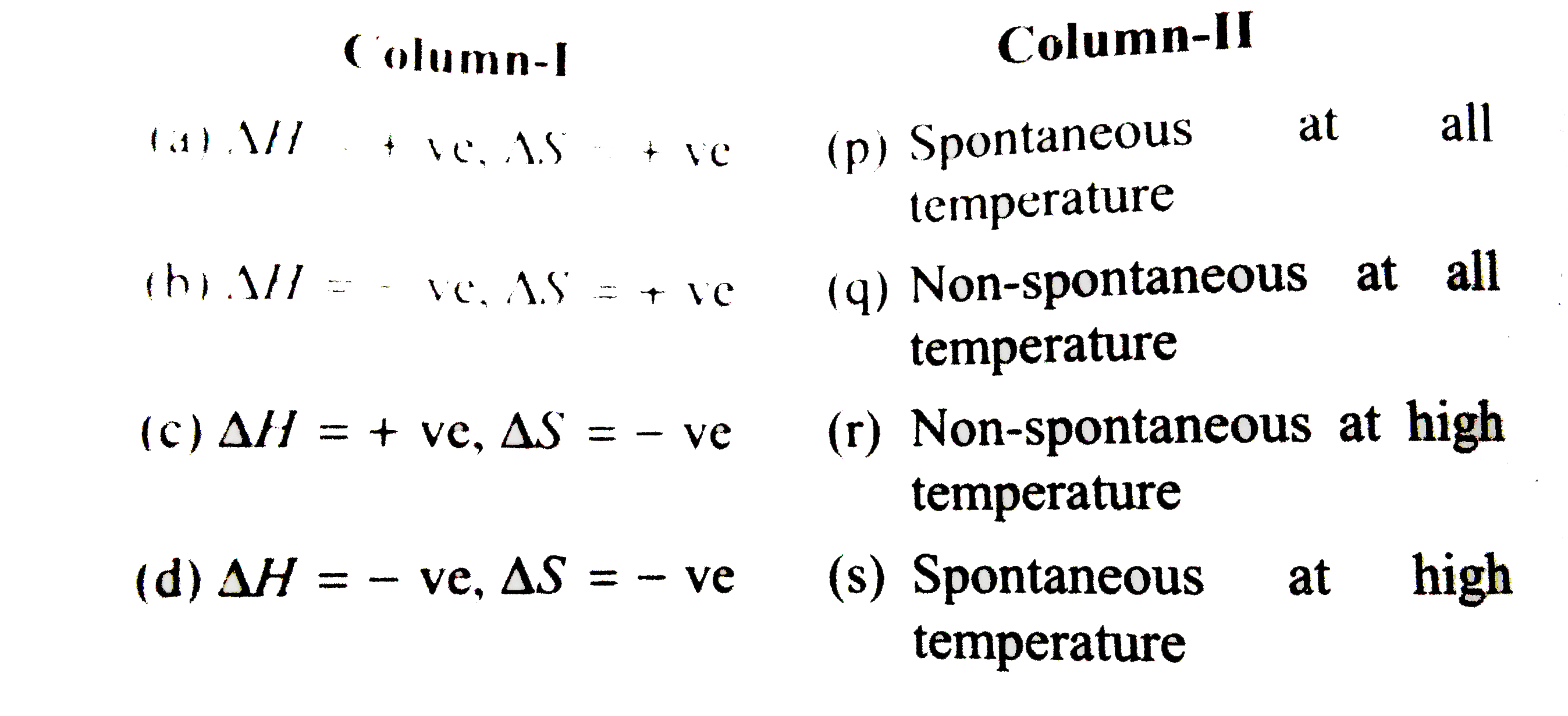
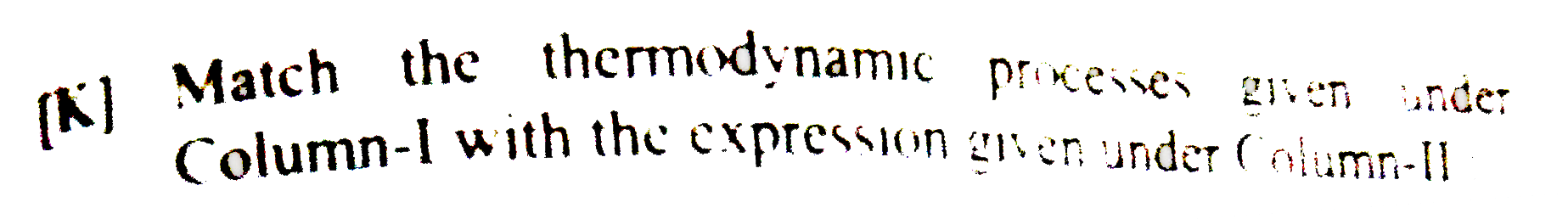

View Solution(i)सिद्ध कीजिए कि आव्यूह A=⎡⎢⎣1−15−121513⎤⎥⎦ एक सममित आव्यूह है।
(ii) सिद्ध कीजिए कि आव्यूह A=⎡⎢⎣01−1−1011−10⎤⎥⎦ एक विषम सममित आव्यूह है।
View SolutionMatch list
List I List IIi.[abba](a)identityii.[0b−b0](b)Singular matrixiii.[aabb](c)Skew-Symmetriciv.[1001](d)Symmetric
The correct match is
(i) (ii) (iii) (iv)
View Solution(i) Show that the matrix A=⎡⎢⎣1−15−121513⎤⎥⎦ is a symmetric matrix.
Show that the matrix A=⎡⎢⎣01−1−1011−10⎤⎥⎦ is a skew symmetric matrix
View SolutionFor the matrix A=[1567], verify that.(i) (A+A′)is a symmetric matrix(ii) (A−A′)is a skew symmetric matrix
View SolutionThe matrix A=[0−585012−8−120] is a (a) diagonal matrix (b) symmetric matrix (c) skew-symmetric matrix (d) scalar matrix
View SolutionThe matrix A=⎡⎢⎣−5−8035012−1⎤⎥⎦ is (A) idempotent matrix (B) involutory matrix (C) nilpotent matrix (D) none of these
View SolutionExpress the matrix [3−2−43−2−5−112] as the sum of a symmetric and skew-symmetric matrix.
View Solution
