Show that r1(s−a)=r2(s−b)=r3(s−c)=Δ
The correct Answer is:∴r1(s−a)=r2(s−b)=r3(s−c)=Δ
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE - 9.1 ( VERY SHORT ANSWER QUESTIONS
17 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE - 9.1 ( SHORT ANSWER QUESTIONS)
16 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
In ABC, show that a2(s−a)+b2(s−b)+c2(s−c))=4R(a+rsin(A2)sin(B2)sin(C2))
View Solutionshow that r2r3+r3r1+r1r2=s2
View SolutionThe exradii r1,r2,r3 of ΔABC and in HP, show that it’s the arithmetic mean of a and c.
View SolutionProve that : r1(s−b)(s−c)+r2(s−c)(s−a)+r3(s−a)(s−b)=3r
View SolutionIf in ΔABC,(a−b)(s−c)=(b−c)(s−a), prove that r1,r2,r3 are in A.P.
View SolutionIf in ΔABC,(a−b)(s−c)=(b−c)(s−a), prove that r1,r2,r3 are in A.P.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
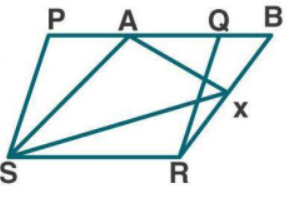
View SolutionIf Sr denotes the sum of the first r terms of an A.P., then show that S3r−Sr−1S2r−S2r−1 is equals
View SolutionIf in ΔABC,(a−b)(s−c)=(b−c)(s−a), prove that r1,r2,r3 are in A.P.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(∣∣gmPQRS)=ar(∣∣gmABRS), ar(△AXS)=12ar(∣∣gmPQRS)
View Solution
