Two identical solid cylinders are released from the top of two inclined planes of equal angles. If one cylinder is in pure rolling and other is in pure sliding motion then
The sliding cylinder will reach the bottom later with lower speed
The rolling cylinder will reach the bottom later with lower speed
Both reach the bottom simultaneously with different speed
Both reach the bottom simultaneously with same speed
To solve the problem, we need to analyze the motion of two identical solid cylinders on inclined planes: one undergoing pure rolling motion and the other undergoing pure sliding motion. Here’s a step-by-step solution:
Step 1: Understanding the Motion
- Pure Rolling Motion: In this case, the cylinder rolls without slipping. The total mechanical energy is conserved, and part of the gravitational potential energy is converted into translational kinetic energy and rotational kinetic energy.
- Pure Sliding Motion: The cylinder slides down the incline without rolling. Here, all the gravitational potential energy is converted into translational kinetic energy.
Step 2: Deriving the Speed for Rolling Cylinder
For a rolling cylinder, the speed V at the bottom of the incline can be derived from energy conservation:
V=
⎷2gh1+k2r2
Where:
- g = acceleration due to gravity
- h = height of the incline
- k = radius of gyration
- r = radius of the cylinder
Step 3: Deriving the Speed for Sliding Cylinder
For a sliding cylinder, the speed Vs at the bottom of the incline is given by:
Vs=√2gh
This is because all potential energy is converted into translational kinetic energy.
Step 4: Comparing the Speeds
From the equations derived:
- The speed of the rolling cylinder V is less than the speed of the sliding cylinder Vs because:
2gh1+k2r2<2gh
This implies that the rolling cylinder will have a lower speed compared to the sliding cylinder.
Step 5: Determining the Time Taken
The time taken t to reach the bottom can be expressed as:
t=dV
Where d is the distance along the incline.
- For the rolling cylinder:
trolling=dV
- For the sliding cylinder:
tsliding=dVs
Step 6: Conclusion
Since Vs>V, it follows that:
tsliding<trolling
Thus, the sliding cylinder reaches the bottom of the incline first, while the rolling cylinder reaches later and at a slower speed.
Final Answer
The sliding cylinder will reach the bottom first, and the rolling cylinder will reach later at a slower speed.
---
- Pure Rolling Motion: In this case, the cylinder rolls without slipping. The total mechanical energy is conserved, and part of the gravitational potential energy is converted into translational kinetic energy and rotational kinetic energy.
- Pure Sliding Motion: The cylinder slides down the incline without rolling. Here, all the gravitational potential energy is converted into translational kinetic energy.
For a rolling cylinder, the speed V at the bottom of the incline can be derived from energy conservation:
V=
⎷2gh1+k2r2
Where:
- g = acceleration due to gravity
- h = height of the incline
- k = radius of gyration
- r = radius of the cylinder
For a sliding cylinder, the speed Vs at the bottom of the incline is given by:
Vs=√2gh
This is because all potential energy is converted into translational kinetic energy.
From the equations derived:
- The speed of the rolling cylinder V is less than the speed of the sliding cylinder Vs because:
2gh1+k2r2<2gh
This implies that the rolling cylinder will have a lower speed compared to the sliding cylinder.
The time taken t to reach the bottom can be expressed as:
t=dV
Where d is the distance along the incline.
trolling=dV
- For the sliding cylinder:
tsliding=dVs
Since Vs>V, it follows that:
tsliding<trolling
Thus, the sliding cylinder reaches the bottom of the incline first, while the rolling cylinder reaches later and at a slower speed.
The sliding cylinder will reach the bottom first, and the rolling cylinder will reach later at a slower speed.
Similar Questions
Two identical cylinders 'runa race' starting from rest at the top of an inclined plane, one slides without rolling and other rolls without slipping. Assuming that no mechanical energy is dissipated in heat, which one will win ?
View SolutionA solid cylinder and ring are released from rest in top of inclined plane. Find ratio of their velocities when they reach bottom,assuming pure rolling
View Solution
Knowledge Check
Two identical solid cylinders run a race starting from rest at the top of an inclined plane. If one cylinder slides and the other rolls :
ASliding cylinder will reach the bottom first with greater speed.BRolling cylinder will reach the bottom first with greater speed.CBoth will reach the bottom simultaneously with the same speed.DBoth will reach the bottom simultaneously but with different speeds.Two solid discs of radii r and 2r roll from the top of an inclined plane without slipping. Then
AThe bigger disc will reach the horizontal level firstBThe smaller disc will reach the horizontal level firstCThe time difference or reaching of the discs at the horizontal level will depend on the inclination of the planeDBoth the discs will reach at the same timeA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced
A and B are two identical rings released from the top of an inclined plane . A slides down and B rolls down. Then which reaches the bottom first ?
View SolutionA solid sphere is in pure rolling motion on an inclined surface having inclination θ

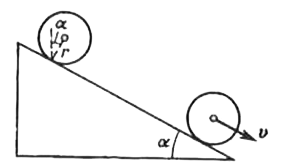
View SolutionA solid cylinder with base radius jis placed on top of an inclined plane of length land slope angle α (Fig). The cylinder rolls down without slipping. Find the speed of the centre of mass of the cylinder at the bottom of the plane, if the coefficient of rolling friction is k. Can rolling friction be neglected? Do the calculation for the following conditions: l=1m,α=30∘,r=10cm,k=5×10−4m . What would be the speed if, in the absence of friction, the cylinder slides down?
View SolutionA solid sphere, a hollow sphere and a dise are released from the top of a frictionless inclined plane so that they slide down the inclined plane (without rolling). The maximum acceleration down the plane is
View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length l. If the cylinder roles without slipping, its speed at the bottom
View Solution
