A uniform magnetic field along a long cylindrical rod varies with time as (B=αt), where α is positive constant. The electric field inside the rod as a function of radial distance r from the central axis is proportional to
r2
1/r
1r2
r
To solve the problem, we need to analyze the relationship between the changing magnetic field and the induced electric field inside the cylindrical rod. Here’s a step-by-step solution:
Step 1: Understand the Given Magnetic Field
The magnetic field B is given as a function of time:
B=αt
where α is a positive constant.
Step 2: Calculate the Rate of Change of Magnetic Field
To find the induced electric field, we first need the rate of change of the magnetic field with respect to time:
dBdt=α
This indicates that the magnetic field is increasing at a constant rate.
Step 3: Use Faraday’s Law of Electromagnetic Induction
According to Faraday's law, the electromotive force (EMF) induced in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
EMF=−dΦdt
where Φ is the magnetic flux.
Step 4: Calculate the Magnetic Flux
The magnetic flux Φ through a circular area of radius r is given by:
Φ=B⋅A=B⋅πr2
Substituting B=αt:
Φ=αt⋅πr2
Step 5: Differentiate the Magnetic Flux with Respect to Time
Now, we differentiate the magnetic flux Φ with respect to time t:
dΦdt=ddt(αt⋅πr2)=απr2
Step 6: Substitute into the EMF Equation
Now substituting dΦdt into the EMF equation:
EMF=−απr2
Step 7: Relate EMF to Electric Field
The EMF can also be expressed in terms of the electric field E and the path length dL:
EMF=E⋅(2πr)
Setting the two expressions for EMF equal to each other:
E⋅(2πr)=−απr2
Step 8: Solve for the Electric Field E
Now, we can solve for the electric field E:
E=−απr22πr=−αr2
This shows that the electric field E is proportional to the radial distance r.
Conclusion
The electric field inside the rod as a function of radial distance r is proportional to r.
Final Answer
The electric field E is proportional to r:
E∝r
The magnetic field B is given as a function of time:
B=αt
where α is a positive constant.
To find the induced electric field, we first need the rate of change of the magnetic field with respect to time:
dBdt=α
This indicates that the magnetic field is increasing at a constant rate.
According to Faraday's law, the electromotive force (EMF) induced in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
EMF=−dΦdt
where Φ is the magnetic flux.
The magnetic flux Φ through a circular area of radius r is given by:
Φ=B⋅A=B⋅πr2
Substituting B=αt:
Φ=αt⋅πr2
Now, we differentiate the magnetic flux Φ with respect to time t:
dΦdt=ddt(αt⋅πr2)=απr2
Now substituting dΦdt into the EMF equation:
EMF=−απr2
The EMF can also be expressed in terms of the electric field E and the path length dL:
EMF=E⋅(2πr)
Setting the two expressions for EMF equal to each other:
E⋅(2πr)=−απr2
Now, we can solve for the electric field E:
E=−απr22πr=−αr2
This shows that the electric field E is proportional to the radial distance r.
The electric field inside the rod as a function of radial distance r is proportional to r.
The electric field E is proportional to r:
E∝r
Similar Questions
A long round dielectric cyclinder is polarized so that teh vector P=αr, where α is a positive constant and r is the distance from the axis. Find the space density ρ' of bound chagres as a function of distance r from the axis.
View SolutionThere exists a uniform cylindrically symmetric magnetic field directed along the axis of a cylinder but varying with time as B=kt. If an electron is released from rest in this field at a distance of 'r' from the axis of cylinder, its acceleration, just after it is released would be (e and m are the electronic charge and mass respectively)
View Solution
Knowledge Check
The displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.Ago on decreasing with timeBbe independent of α and βCdrop to zero when α =βDgo on increasing with time.The magnitude of radius vector of a point varies with time as r=βt(1−αt) where α and β are positive constant. The distance travelled by this body over a closed path must be
AβαBβ2αCαβD2αβA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
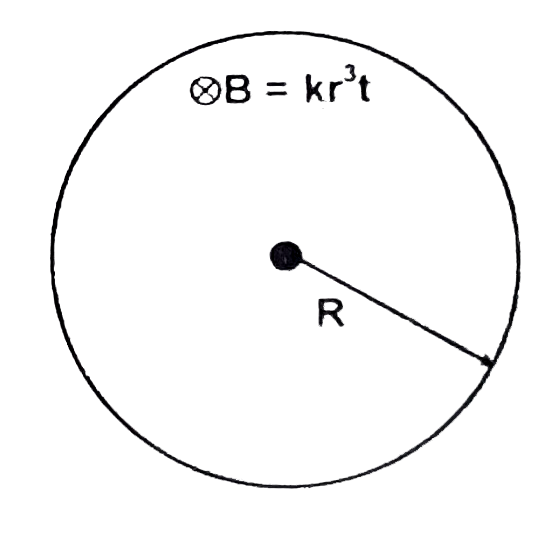 AKR420BKR440CKR460DKR480
AKR420BKR440CKR460DKR480
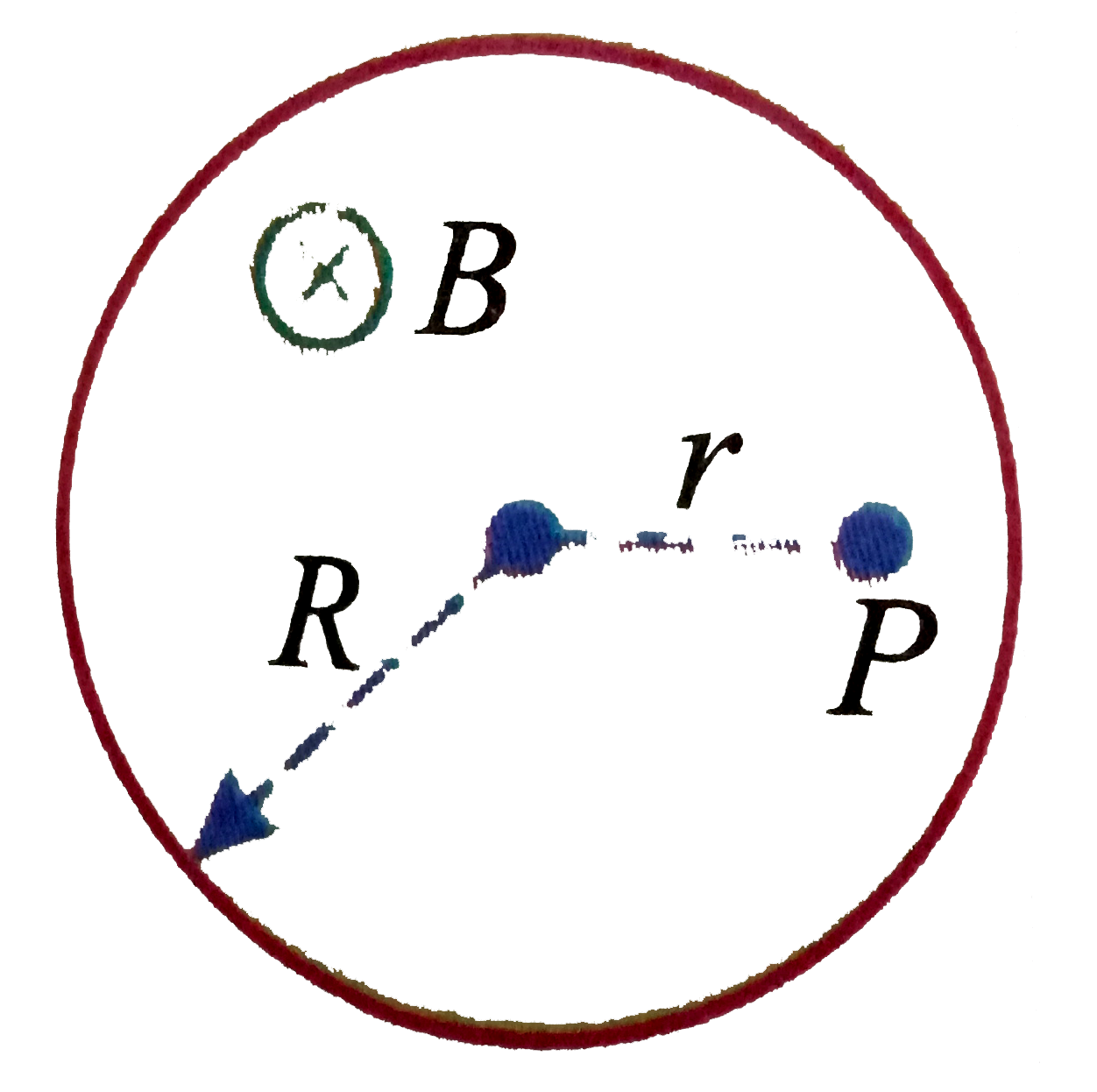
A uniform magentic field of induction B is confined in a cyclinderical region of radius R. If the field is incresing at a constant rate of dBdt=αT/s, then the intensity of the electric field induced at point P, distant r from the axis as shown in the figure is proportional to :
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is
View SolutionAn infinitely long hollow conducting cylinder with inner radius r2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionA time varying uniform magnetic field passes through a circular region of radius R. The magnetic field is directed outwards and it is a function of radial distance 'r' and time 't' according to relation B-B_(0)rt. The induced electric field strength at a radial distance R/2 from the centre will be.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View Solution
