A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/s2)
136N
116N
265N
Zero
The correct Answer is:d
To find the tension in the string when the particle is revolving in a horizontal circle, we can follow these steps:
Step 1: Identify the given values
- Mass of the particle, m=200g=0.2kg (since 1 g = 0.001 kg)
- Length of the string, L=1.30m
- Radius of the horizontal circle, r=50cm=0.5m
- Acceleration due to gravity, g=10m/s2
Step 2: Determine the vertical and horizontal components of forces
When the particle is revolving in a horizontal circle, the tension in the string has two components:
1. A vertical component that balances the weight of the particle.
2. A horizontal component that provides the centripetal force required for circular motion.
Step 3: Calculate the weight of the particle
The weight W of the particle can be calculated using the formula:
W=m⋅g
Substituting the values:
W=0.2kg⋅10m/s2=2N
Step 4: Use the geometry of the system
In this scenario, we can use the geometry of the string. The vertical component of the tension T must balance the weight of the particle, and the horizontal component provides the centripetal force.
The vertical component of the tension is given by:
Tv=T⋅cos(θ)
And the horizontal component is given by:
Th=T⋅sin(θ)
Where θ is the angle the string makes with the vertical.
Step 5: Find θ
Using the right triangle formed by the string, the vertical line, and the radius:
cos(θ)=L−rL=1.30−0.51.30=0.81.30≈0.6154
sin(θ)=√1−cos2(θ)=√1−(0.6154)2≈√1−0.3787≈√0.6213≈0.789
Step 6: Set up the equations
From the vertical forces:
T⋅cos(θ)=W
Substituting the known values:
T⋅0.6154=2
Thus,
T=20.6154≈3.24N
Step 7: Conclusion
The tension in the string is approximately 3.24N.
---
- Mass of the particle, m=200g=0.2kg (since 1 g = 0.001 kg)
- Length of the string, L=1.30m
- Radius of the horizontal circle, r=50cm=0.5m
- Acceleration due to gravity, g=10m/s2
When the particle is revolving in a horizontal circle, the tension in the string has two components:
1. A vertical component that balances the weight of the particle.
2. A horizontal component that provides the centripetal force required for circular motion.
The weight W of the particle can be calculated using the formula:
W=m⋅g
Substituting the values:
W=0.2kg⋅10m/s2=2N
In this scenario, we can use the geometry of the string. The vertical component of the tension T must balance the weight of the particle, and the horizontal component provides the centripetal force.
Tv=T⋅cos(θ)
And the horizontal component is given by:
Th=T⋅sin(θ)
Using the right triangle formed by the string, the vertical line, and the radius:
cos(θ)=L−rL=1.30−0.51.30=0.81.30≈0.6154
sin(θ)=√1−cos2(θ)=√1−(0.6154)2≈√1−0.3787≈√0.6213≈0.789
From the vertical forces:
T⋅cos(θ)=W
Substituting the known values:
T⋅0.6154=2
Thus,
T=20.6154≈3.24N
The tension in the string is approximately 3.24N.
Topper's Solved these Questions
Similar Questions
A sphere of mass 200 g is attached to an inextensible string of length 130 cm whose upper end is fixed to the ceilling . The sphere is made to describe a horizontal circle of radius 50 cm Calculate the periodic time of this conical pendulum and the tension in the string .
View SolutionA sphere of mass0.1kg is attached to an inextensible string of length 1.3m whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius 0.5m Calculate time period of revolution and tension in the string .
View Solution
Knowledge Check
A particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A2π√ghB√g/hC2π√h/gD12π√g/hA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
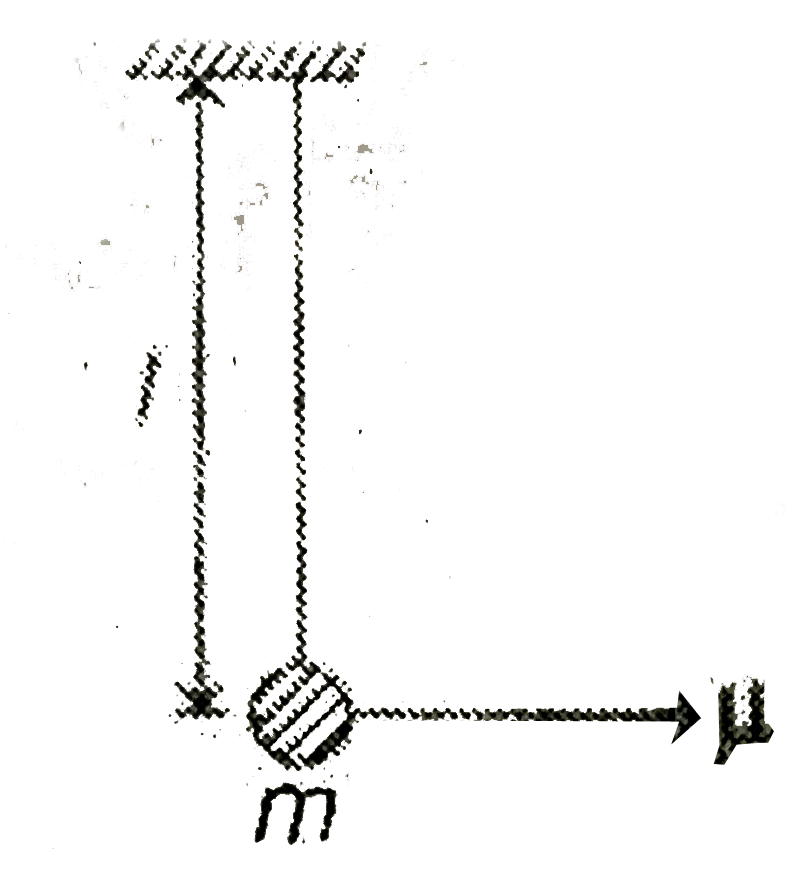
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isAmgB2 mgC4 mgD6 mg
A particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.
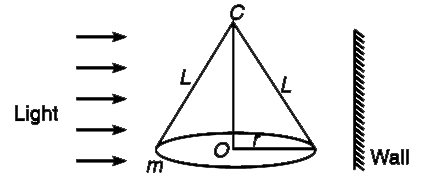
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall.
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, find the tension in the string.
View SolutionA stone of mass 50 g is tied to the end of a string 2 m long and is set into rotation in a horizontal circle with a uniforn speed of 2m/s .Then tension in the string is
View Solution
