The ratio of the density and pressure of a fixed mass of an ideal gas is "5" at 10°C. Then this ratio at 110°C is
3.69
5
8.46
6.76
The correct Answer is:A
To solve the problem, we need to find the ratio of density (ρ) and pressure (P) of an ideal gas at two different temperatures. We are given that the ratio at 10°C (283 K) is 5, and we need to find the ratio at 110°C (383 K).
1. Identify the Given Values:
- The ratio of density to pressure at 10°C (T1 = 283 K) is given as:
ρP=R1=5
- The temperature at 10°C in Kelvin:
T1=10+273=283 K
- The temperature at 110°C in Kelvin:
T2=110+273=383 K
2. Use the Ideal Gas Law:
The ideal gas law states:
P=ρRTM
Rearranging gives:
ρP=RTM
This shows that the ratio of density to pressure is directly proportional to the temperature (T).
3. Set Up the Proportionality:
Since we know that:
ρP∝T
We can write the ratios at the two temperatures:
R1R2=T1T2
4. Substitute the Known Values:
Substitute the known values into the equation:
5R2=283383
5. Cross-Multiply to Solve for R2:
Cross-multiplying gives:
5⋅383=R2⋅283
1915=R2⋅283
Now, solving for R2:
R2=1915283≈6.76
6. Final Result:
Thus, the ratio of density to pressure at 110°C is approximately:
R2≈6.76
Conclusion:
The ratio of density to pressure of the ideal gas at 110°C is approximately 6.76.
- The ratio of density to pressure at 10°C (T1 = 283 K) is given as:
ρP=R1=5
- The temperature at 10°C in Kelvin:
T1=10+273=283 K
- The temperature at 110°C in Kelvin:
T2=110+273=383 K
The ideal gas law states:
P=ρRTM
Rearranging gives:
ρP=RTM
This shows that the ratio of density to pressure is directly proportional to the temperature (T).
Since we know that:
ρP∝T
We can write the ratios at the two temperatures:
R1R2=T1T2
Substitute the known values into the equation:
5R2=283383
Cross-multiplying gives:
5⋅383=R2⋅283
1915=R2⋅283
Now, solving for R2:
R2=1915283≈6.76
Thus, the ratio of density to pressure at 110°C is approximately:
R2≈6.76
The ratio of density to pressure of the ideal gas at 110°C is approximately 6.76.
Topper's Solved these Questions
Similar Questions
Knowledge Check
At 10∘C, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at 110∘C, this ratio is
AxB383283xC10110xD283383xFor a fixed mass of an ideal gas the correct representation is:
A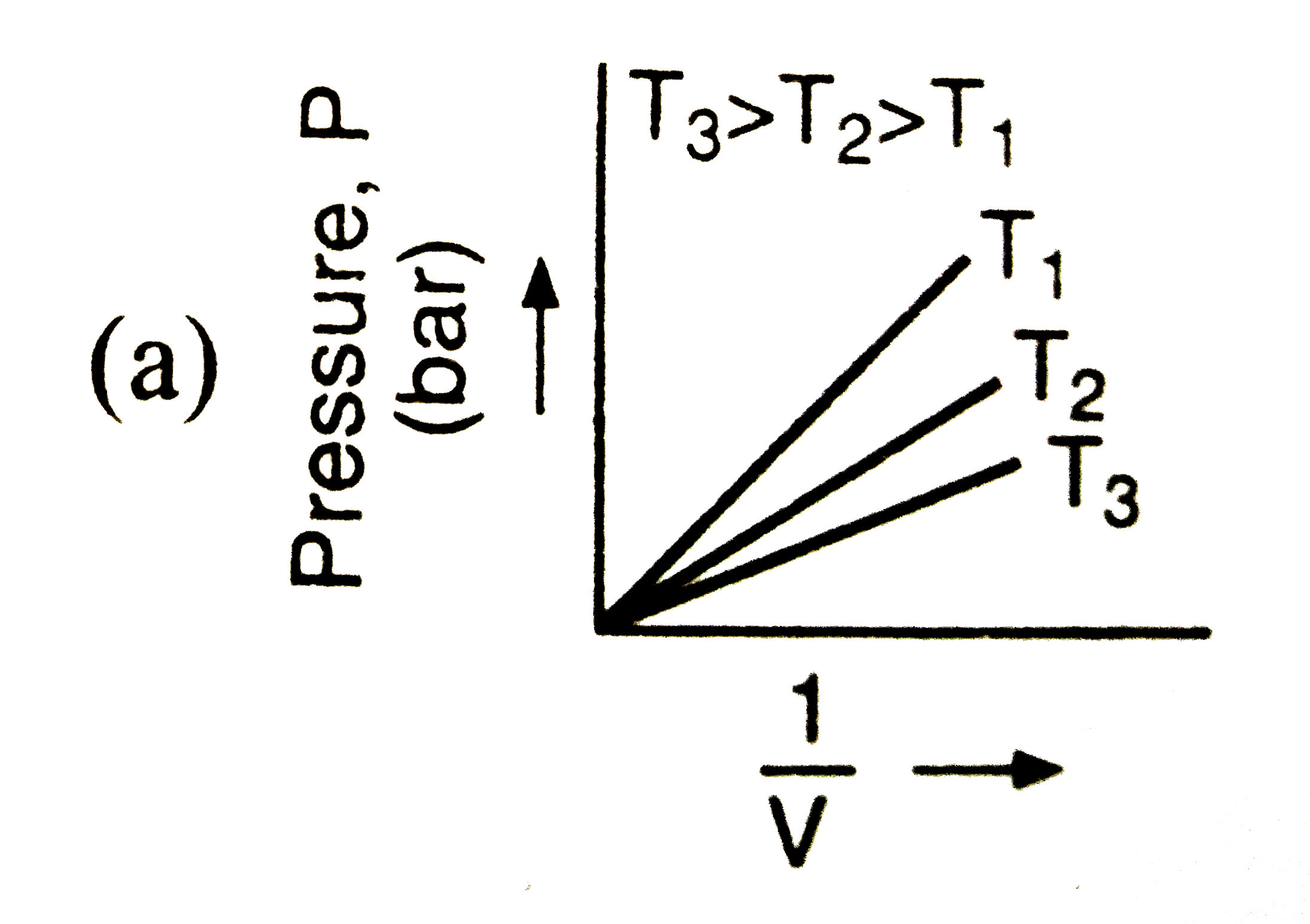 B
B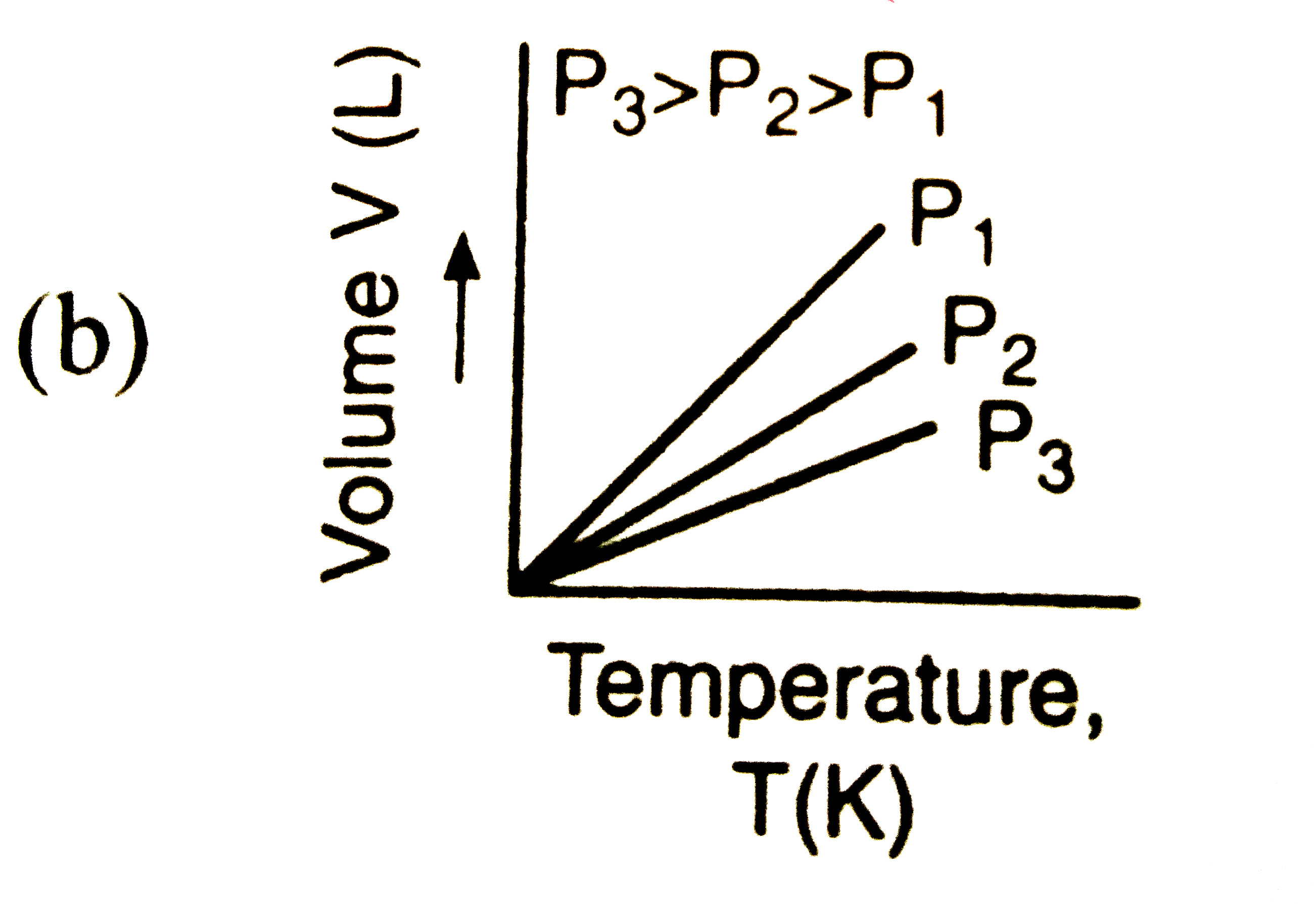 C
C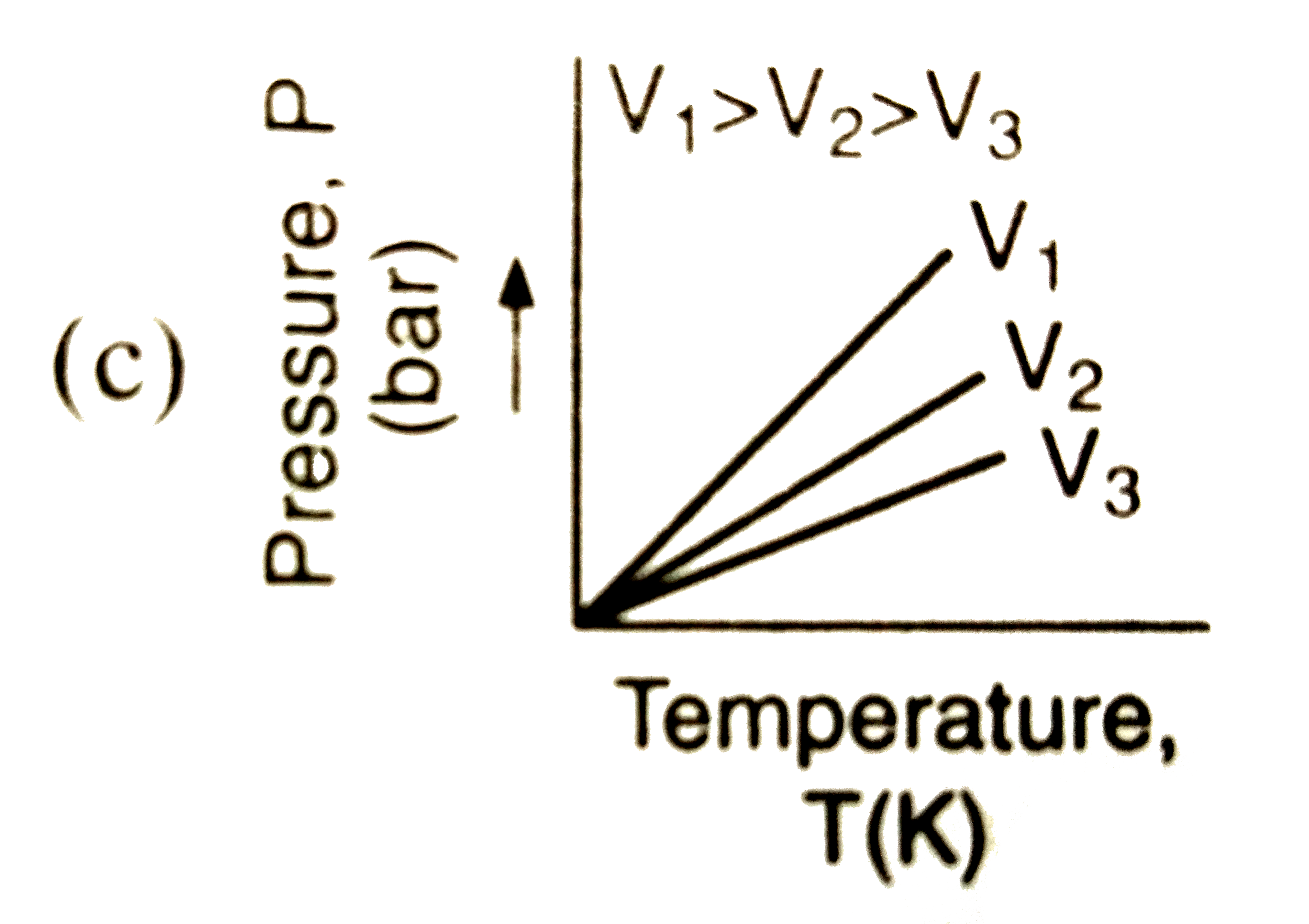 D
D
At 10∘C, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at 110∘C, this ratio is
A283383xBxC383283xD10110x
At constant pressure , the volume of fixed mass of an ideal gas is directly proportional to
View SolutionAt 10∘C, the density of a fixed mass of an ideal gas divided by its pressure is X. At 110∘C, this ratio would be
View SolutionA 0∘C the density of a fixed mass of a gas divided by pressure is x. At 100∘C, the ratio will be
View SolutionDuring an adiabatic process , the pressure p of a fixed mass of an ideal gas change by Δpand its volume V change by ΔV . If γ=Cp/Cv then ΔV/V is given by
View SolutionIf E is the energy density in an ideal gas, then the pressure of the ideal gas is
View Solution