Two blocks A and B of same material and of masses m and 2m moving with same kinetic energy on a surface enter in a region of identical rough surface. Choose the correct statement from the following options.
A will move more distance before stopping
B will move more distance before stopping
Both will move same distance before stopping
Both will never stop
To solve the problem of two blocks A and B of masses m and 2m moving with the same kinetic energy on a rough surface, we can follow these steps:
Step 1: Understand the Kinetic Energy
Both blocks A and B have the same kinetic energy. The kinetic energy (KE) is given by the formula:
KE=12mv2
Let the velocity of block A be v1 and the velocity of block B be v2. Since both blocks have the same kinetic energy, we can write:
12mv21=12(2m)v22
This simplifies to:
v21=2v22
Step 2: Relate the Velocities
From the equation v21=2v22, we can express v1 in terms of v2:
v1=√2v2
Step 3: Determine the Acceleration due to Friction
The acceleration a due to friction for both blocks can be expressed as:
a=Fm=μg
where μ is the coefficient of friction and g is the acceleration due to gravity. This means both blocks will experience the same deceleration due to friction.
Step 4: Use the Kinematic Equation
Using the kinematic equation s=v22a to find the stopping distance for both blocks:
- For block A:
s1=v212a=v212μg
- For block B:
s2=v222a=v222μg
Step 5: Substitute the Velocities
Substituting v21=2v22 into the equation for s1:
s1=2v222μg=v22μg
Now we have:
s1=v22μgands2=v222μg
Step 6: Find the Ratio of Distances
Now, we can find the ratio of the distances s1 and s2:
s1s2=v22μgv222μg=2
This means:
s1=2s2
Conclusion
Block A, which has a mass m and a higher velocity, will travel twice the distance of block B before coming to a stop on the rough surface. Therefore, the correct statement is that block A will move more distance before stopping.
Both blocks A and B have the same kinetic energy. The kinetic energy (KE) is given by the formula:
KE=12mv2
Let the velocity of block A be v1 and the velocity of block B be v2. Since both blocks have the same kinetic energy, we can write:
12mv21=12(2m)v22
This simplifies to:
v21=2v22
From the equation v21=2v22, we can express v1 in terms of v2:
v1=√2v2
The acceleration a due to friction for both blocks can be expressed as:
a=Fm=μg
where μ is the coefficient of friction and g is the acceleration due to gravity. This means both blocks will experience the same deceleration due to friction.
Using the kinematic equation s=v22a to find the stopping distance for both blocks:
- For block A:
s1=v212a=v212μg
- For block B:
s2=v222a=v222μg
Substituting v21=2v22 into the equation for s1:
s1=2v222μg=v22μg
Now we have:
s1=v22μgands2=v222μg
Now, we can find the ratio of the distances s1 and s2:
s1s2=v22μgv222μg=2
This means:
s1=2s2
Block A, which has a mass m and a higher velocity, will travel twice the distance of block B before coming to a stop on the rough surface. Therefore, the correct statement is that block A will move more distance before stopping.
Similar Questions
Knowledge Check
A sharp vertical impulse J is given to a uniform solid sphere of mass m and radius R place on a rough horizontal surface. Choose the correct options
 AImpulse imparted to the sphere by the surface perpendicular to te suurface will also have magnitude JBMinimum value of coefficient of friction between sphere and surface to avoid slipping is μ=47CIf μ=1120, sphere rols with backward slippingDIf μ=1320 sphere rolls with forward slipping
AImpulse imparted to the sphere by the surface perpendicular to te suurface will also have magnitude JBMinimum value of coefficient of friction between sphere and surface to avoid slipping is μ=47CIf μ=1120, sphere rols with backward slippingDIf μ=1320 sphere rolls with forward slippingA proton, a deuteron and an α-particle with the same KE enter a region of uniform magnetic field, moving at right angles to B. What is the ratio of the radii of their circular paths ?
A1:√2:1B1:√2:√2C√2:1:1D√2:√2:1Two block of same mass m undergo headon collision as shown. E is the coefficient of restitution. Choose the correct statement(s) :
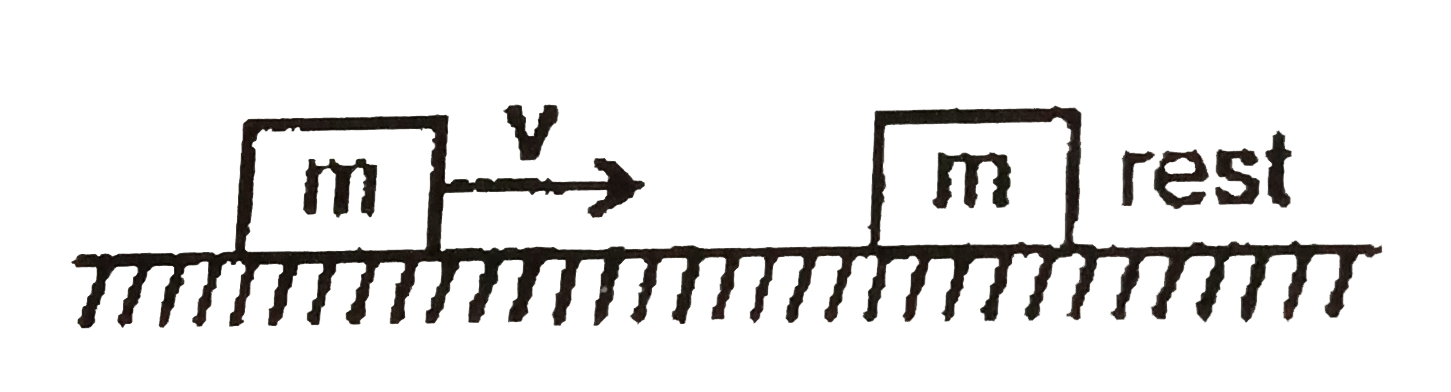 AIf e = 1, just after collision KE of right block is 12mv2.BIf e = 0, loss in KE is 12(mv22).CIf e = 12, loss in KE = 316mv2.DNo impulsive force acts on left block during collision.
AIf e = 1, just after collision KE of right block is 12mv2.BIf e = 0, loss in KE is 12(mv22).CIf e = 12, loss in KE = 316mv2.DNo impulsive force acts on left block during collision.
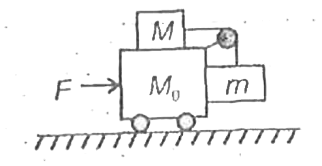
Two blocks of mass M and m are kept on the trolley whose all surfaces are smooth select the correct statement
View SolutionTwo bodies A and B having mass m and M respectively ppossess same kinetic energy. Given that M>m. If pA and pB be their moments, then which of the following statements is true?
View Solution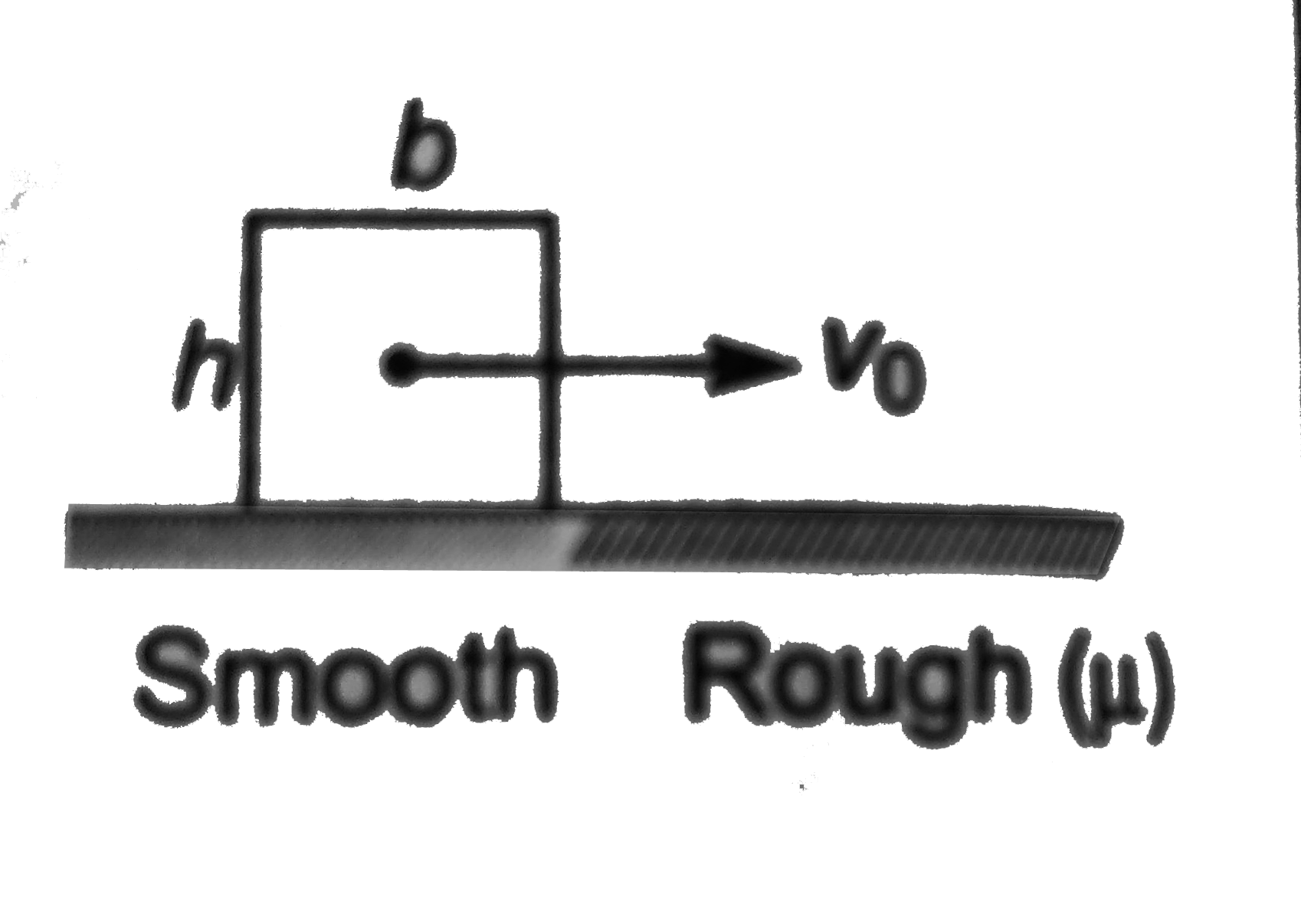
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).

View SolutionTwo bodies of masses m and 2m have same momentum. Their respective kinetic energies E1 and E2 are in the ratio
View Solution
