A particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
136N
116N
265N
Zero
To find the tension in the string when a particle is revolving in a horizontal circle, we can follow these steps:
Step 1: Identify the Given Values
- Mass of the particle, m=200g=0.2kg
- Length of the string, L=1.30m
- Radius of the horizontal circle, r=50cm=0.5m
- Acceleration due to gravity, g=10m/s2
Step 2: Determine the Vertical and Horizontal Components of Forces
When the particle is revolving, the tension in the string has two components:
- A vertical component that balances the weight of the particle.
- A horizontal component that provides the centripetal force required for circular motion.
Step 3: Calculate the Weight of the Particle
The weight of the particle W is given by:
W=m⋅g=0.2kg⋅10m/s2=2N
Step 4: Use Geometry to Relate Tension and Radius
From the geometry of the situation, we can use the right triangle formed by the string, the vertical height, and the radius of the circle. The vertical height h can be calculated as:
h=√L2−r2=√(1.30)2−(0.5)2
Calculating this gives:
h=√1.69−0.25=√1.44=1.2m
Step 5: Apply the Tension Components
Let T be the tension in the string. The vertical component of the tension balances the weight:
T⋅cos(θ)=W
Where θ is the angle between the string and the vertical. We can find cos(θ) using the height:
cos(θ)=hL=1.21.3
Step 6: Calculate the Tension
Now substituting into the equation:
T⋅1.21.3=2N
Solving for T:
T=2⋅1.31.2=2.61.2≈2.17N
Step 7: Conclusion
The tension in the string is approximately 2.17N.
---
- Mass of the particle, m=200g=0.2kg
- Length of the string, L=1.30m
- Radius of the horizontal circle, r=50cm=0.5m
- Acceleration due to gravity, g=10m/s2
When the particle is revolving, the tension in the string has two components:
- A vertical component that balances the weight of the particle.
- A horizontal component that provides the centripetal force required for circular motion.
The weight of the particle W is given by:
W=m⋅g=0.2kg⋅10m/s2=2N
From the geometry of the situation, we can use the right triangle formed by the string, the vertical height, and the radius of the circle. The vertical height h can be calculated as:
h=√L2−r2=√(1.30)2−(0.5)2
Calculating this gives:
h=√1.69−0.25=√1.44=1.2m
Let T be the tension in the string. The vertical component of the tension balances the weight:
T⋅cos(θ)=W
Where θ is the angle between the string and the vertical. We can find cos(θ) using the height:
cos(θ)=hL=1.21.3
Now substituting into the equation:
T⋅1.21.3=2N
Solving for T:
T=2⋅1.31.2=2.61.2≈2.17N
The tension in the string is approximately 2.17N.
Similar Questions
A sphere of mass 200 g is attached to an inextensible string of length 130 cm whose upper end is fixed to the ceilling . The sphere is made to describe a horizontal circle of radius 50 cm Calculate the periodic time of this conical pendulum and the tension in the string .
View SolutionA sphere of mass0.1kg is attached to an inextensible string of length 1.3m whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius 0.5m Calculate time period of revolution and tension in the string .
View Solution
Knowledge Check
A particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A2π√ghB√g/hC2π√h/gD12π√g/hA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
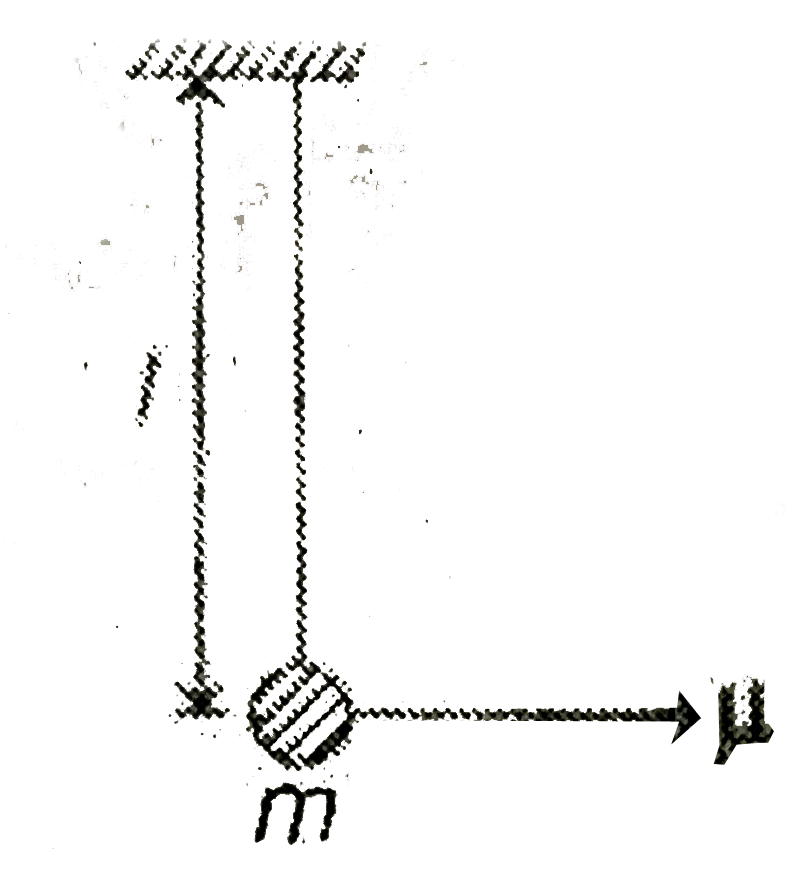
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isAmgB2 mgC4 mgD6 mg
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionA particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.
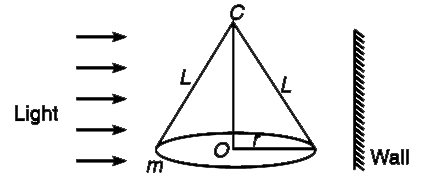
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall.
View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, find the tension in the string.
View SolutionA stone of mass 50 g is tied to the end of a string 2 m long and is set into rotation in a horizontal circle with a uniforn speed of 2m/s .Then tension in the string is
View Solution
