Question

A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.

Explanation

The situation shown in ure. The angle `theta` made by the string with verticla is given by
`sintheta=r/L`………..i

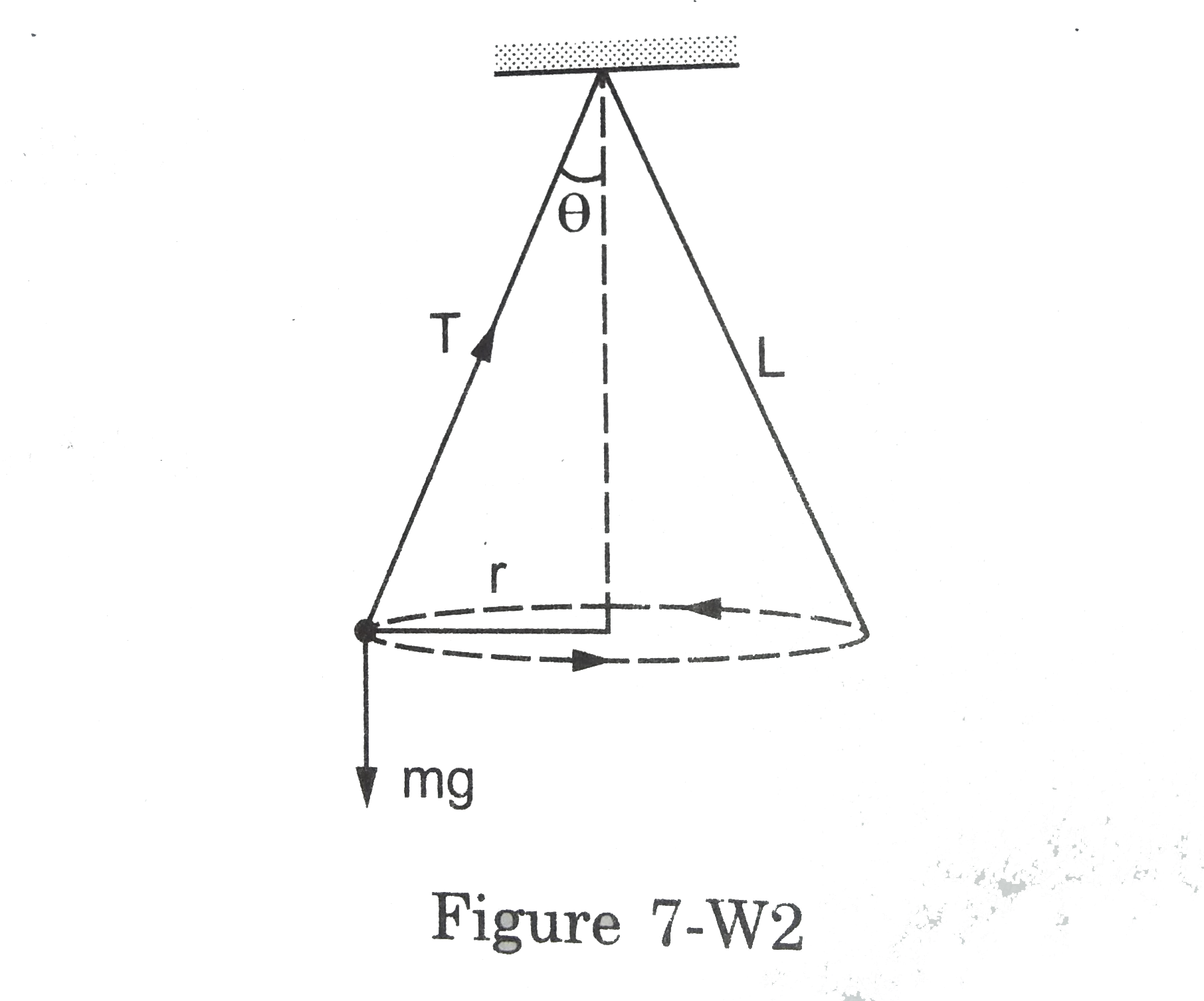
The forces on the pasrticle are
a. the tension T along the string and
b. the weight mg vertically downward.
The particle is moving in a circle with a constant speed v. Thus, the radial acceleration towards the centre has magnitude `v^2/h`. Resolving the forces along the radia direction and applying Newton's second law,
`Tsintheta=m(v^2/r)` ..........ii
As thee is no cceleration in vertical directin we have from Newton's first law
`Tcostheta=mg`...............iii
Dividing ii by iii,
`tantheta=v^2/(rg)`
`or, v=sqrt(rg tantheta)`
and from iii,
`T=(mg)/(costheta)`
using i.
`v=(rsqrtg)/((L^2-r^2)^(1/4)) and T=(mgL)/((L^2-r^2)^(1/2))`