The moment of inertia of a uniform square plate of mass M and edge length a about one of its diagonals is
Ma2
12Ma2
Ma212
Ma23
To find the moment of inertia of a uniform square plate of mass M and edge length a about one of its diagonals, we can follow these steps:
Step 1: Understand the Geometry
We start with a square plate with mass M and edge length a. The square has two diagonals, and we need to find the moment of inertia about one of these diagonals.
Step 2: Use the Parallel Axis Theorem
The moment of inertia about an axis can be calculated using the parallel axis theorem. However, for a square plate, we can directly use known formulas.
Step 3: Moment of Inertia About an Axis in the Plane
For a square plate, the moment of inertia about an axis that is parallel to one of its sides (and passing through its center) is given by:
Iside=13Ma2
Step 4: Moment of Inertia About the Diagonal
The moment of inertia about one of the diagonals can be derived using the perpendicular axis theorem. According to this theorem, for a flat plate:
Iz=Ix+Iy
where Iz is the moment of inertia about an axis perpendicular to the plane, and Ix and Iy are the moments of inertia about two perpendicular axes in the plane.
For our square plate:
Ix=Iy=13Ma2
Thus, the moment of inertia about the perpendicular axis is:
Iz=Ix+Iy=13Ma2+13Ma2=23Ma2
Step 5: Calculate the Moment of Inertia About the Diagonal
Since the moment of inertia about the diagonal Id is related to the moment of inertia about the perpendicular axis Iz by:
Id=12Iz
we can substitute:
Id=12(23Ma2)=13Ma2
Final Result
Thus, the moment of inertia of a uniform square plate of mass M and edge length a about one of its diagonals is:
Id=16Ma2
We start with a square plate with mass M and edge length a. The square has two diagonals, and we need to find the moment of inertia about one of these diagonals.
The moment of inertia about an axis can be calculated using the parallel axis theorem. However, for a square plate, we can directly use known formulas.
For a square plate, the moment of inertia about an axis that is parallel to one of its sides (and passing through its center) is given by:
Iside=13Ma2
The moment of inertia about one of the diagonals can be derived using the perpendicular axis theorem. According to this theorem, for a flat plate:
Iz=Ix+Iy
where Iz is the moment of inertia about an axis perpendicular to the plane, and Ix and Iy are the moments of inertia about two perpendicular axes in the plane.
Ix=Iy=13Ma2
Thus, the moment of inertia about the perpendicular axis is:
Iz=Ix+Iy=13Ma2+13Ma2=23Ma2
Since the moment of inertia about the diagonal Id is related to the moment of inertia about the perpendicular axis Iz by:
Id=12Iz
we can substitute:
Id=12(23Ma2)=13Ma2
Thus, the moment of inertia of a uniform square plate of mass M and edge length a about one of its diagonals is:
Id=16Ma2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The radius of gyration of a uniform square plate of mass M and side a about its diagonal is
Aa√6Ba2√3Ca2√2Da4The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
AI0+ML2/4BI0+2ML2CI0+ML2DI0+ML2/2
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
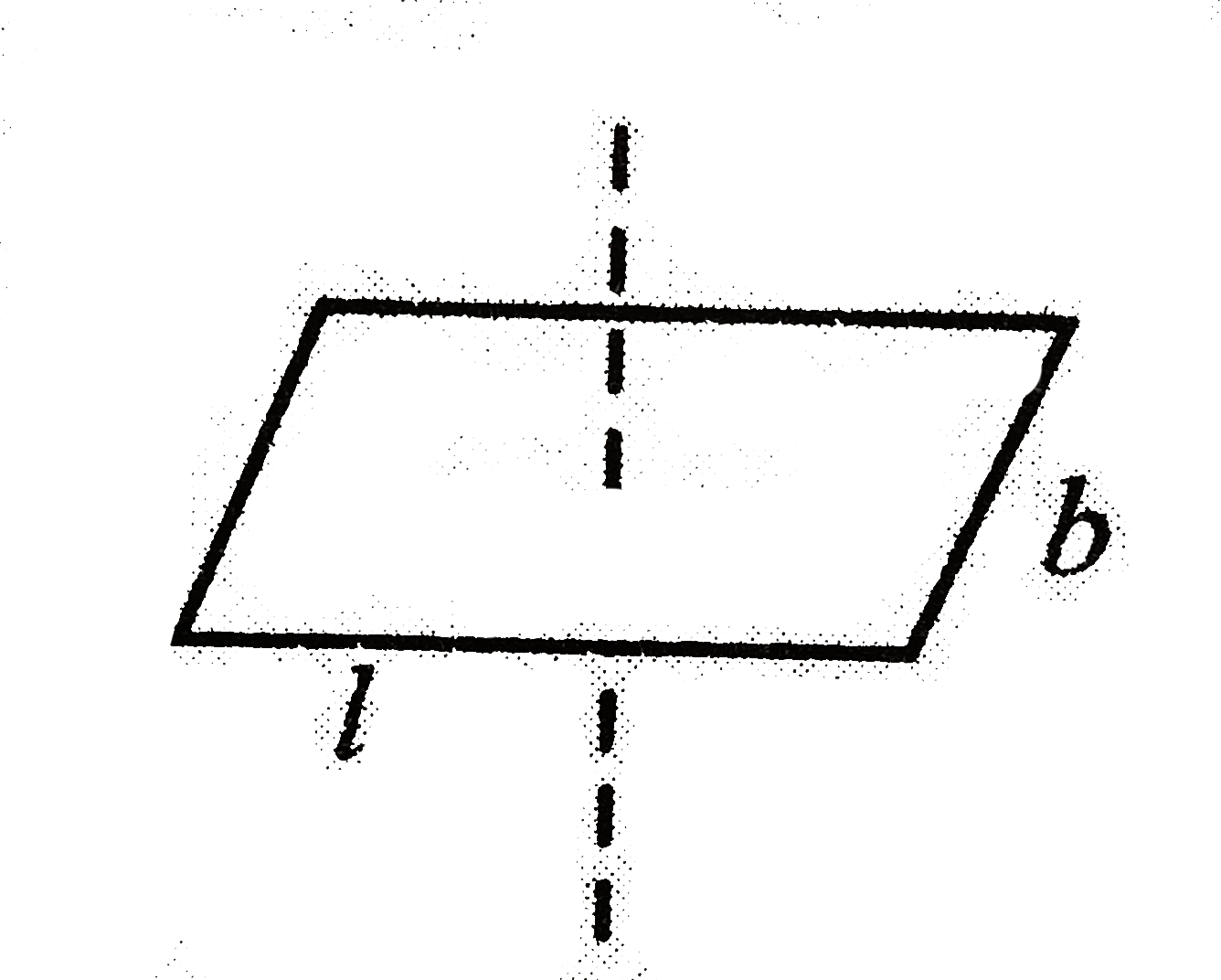
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a uniform solid regular tetrahedron of mass m and edge a, about its symmetry axis (i.e and axis passing through on vertex and the centre of the opposite face) is:
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0 . Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
View Solution