Find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
To find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals, we can use the Perpendicular Axis Theorem. Here’s the step-by-step solution:
Step 1: Understand the Geometry
We have a uniform square plate with mass M and side length a. The diagonals of the square intersect at the center of the square and are perpendicular to each other.
Step 2: Identify the Axes
We will denote:
- I1: Moment of inertia about one diagonal.
- I2: Moment of inertia about the other diagonal.
- I3: Moment of inertia about an axis perpendicular to the plane of the square and passing through the center.
Step 3: Use the Perpendicular Axis Theorem
According to the Perpendicular Axis Theorem, for a planar body:
I3=I1+I2
Since the square plate is uniform, the moment of inertia about both diagonals will be the same, i.e., I1=I2.
Thus, we can rewrite the equation as:
I3=2I1
Step 4: Calculate I3
The moment of inertia of a square plate about an axis perpendicular to its plane and passing through its center is given by:
I3=16Ma2
Step 5: Substitute I3 into the Equation
Now substituting I3 into the equation:
16Ma2=2I1
Step 6: Solve for I1
Now, we can solve for I1:
I1=12(16Ma2)=112Ma2
Conclusion
Thus, the moment of inertia of the uniform square plate about one of its diagonals is:
I=112Ma2
We have a uniform square plate with mass M and side length a. The diagonals of the square intersect at the center of the square and are perpendicular to each other.
We will denote:
- I1: Moment of inertia about one diagonal.
- I2: Moment of inertia about the other diagonal.
- I3: Moment of inertia about an axis perpendicular to the plane of the square and passing through the center.
According to the Perpendicular Axis Theorem, for a planar body:
I3=I1+I2
Since the square plate is uniform, the moment of inertia about both diagonals will be the same, i.e., I1=I2.
I3=2I1
The moment of inertia of a square plate about an axis perpendicular to its plane and passing through its center is given by:
I3=16Ma2
Now substituting I3 into the equation:
16Ma2=2I1
Now, we can solve for I1:
I1=12(16Ma2)=112Ma2
Thus, the moment of inertia of the uniform square plate about one of its diagonals is:
I=112Ma2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective30videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of gyration of a uniform square plate of mass M and side a about its diagonal is
Aa√6Ba2√3Ca2√2Da4 - Question 2 - Select One
The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2 - Question 3 - Select One
The moment of inertia of a cube of mass m and side a about one of its edges is equal to
A23ma2B43ma2C3ma2D83ma2
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.
 View Solution
View SolutionFind the moment of inertia of a uniform rign of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
 View Solution
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
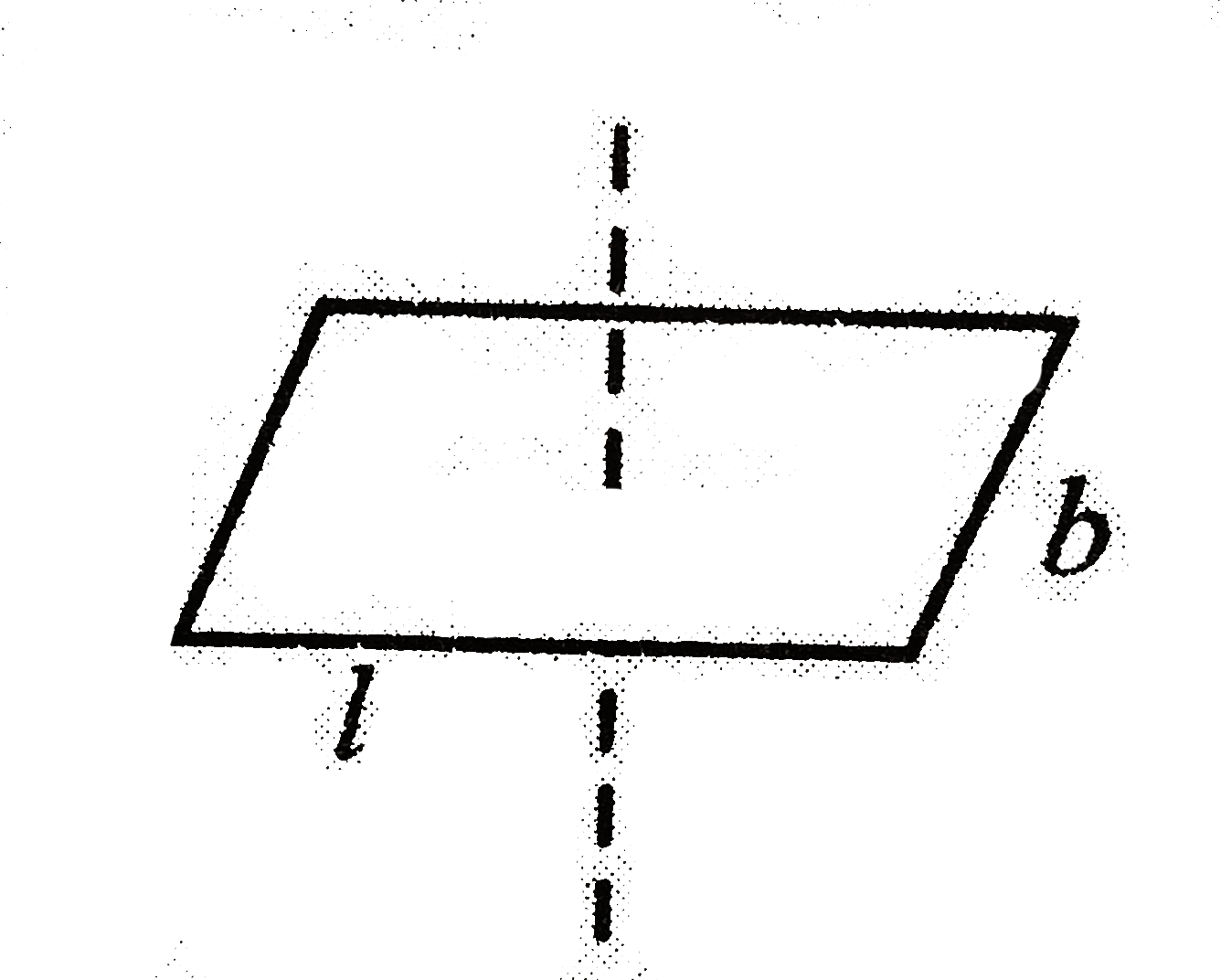 View Solution
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution

