Question

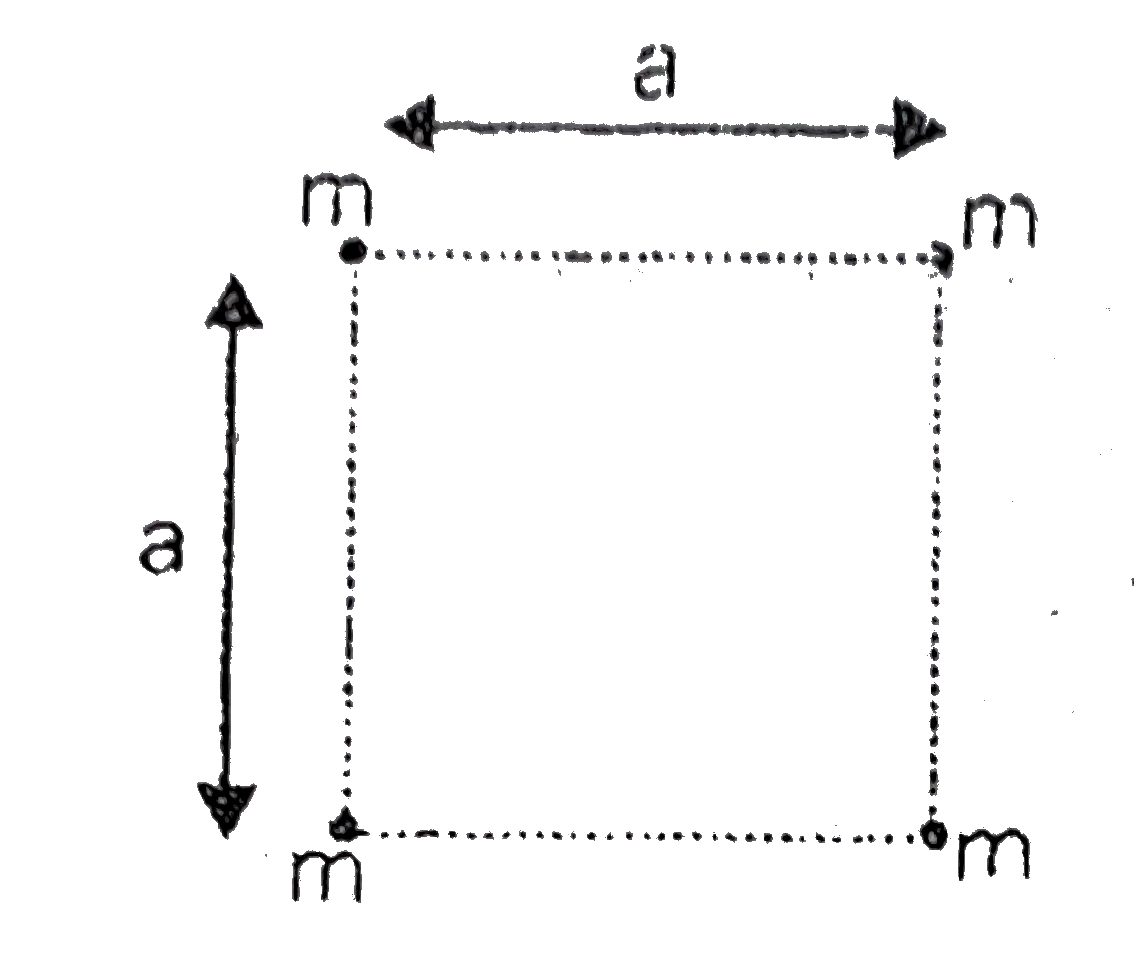
The force between two identical particles separated by distance d is F . Four such identical particles are placed at the corners of a square of side d. The magnitude of net force on any particle will be

Options

A. Zero
B. `(2sqrt2+1)F`
C. `(2√2+1)F/2`
D. `(2sqrt2-1)F/2`

Explanation

To find the net force on any particle placed at the corners of a square formed by four identical particles, we can follow these steps:

Step 1: Understand the Configuration
We have four identical particles placed at the corners of a square with side length \( d \). Let's label the particles as \( A, B, C, \) and \( D \).

Step 2: Identify the Forces Acting on One Particle
Let's consider the force acting on particle \( A \). The forces acting on particle \( A \) are due to particles \( B \) (to the right), \( D \) (below), and \( C \) (diagonally opposite).

Step 3: Calculate the Forces Between the Particles
The force between any two particles separated by distance \( d \) is given as \( F \). Therefore:
- The force between \( A \) and \( B \) is \( F \) (to the right).
- The force between \( A \) and \( D \) is \( F \) (downward).
- The force between \( A \) and \( C \) is also \( F \), but since \( C \) is diagonally opposite, the distance between \( A \) and \( C \) is \( \sqrt{d^2 + d^2} = d\sqrt{2} \).

Step 4: Calculate the Force Between \( A \) and \( C \)
Using the inverse square law, the force between \( A \) and \( C \) can be calculated as:
\( F_{AC} = \frac{F}{2} \quad \text{(since the distance is } d\sqrt{2}\text{)} \)

Step 5: Resolve the Forces into Components
Now, we need to resolve the forces acting on \( A \):
- The force \( F_{AB} \) (to the right) has components:
- \( F_{ABx} = F \)
- \( F_{ABy} = 0 \)

- The force \( F_{AD} \) (downward) has components:
- \( F_{ADx} = 0 \)
- \( F_{ADy} = F \)

- The force \( F_{AC} \) (diagonal) can be resolved into components:
- \( F_{ACx} = \frac{F}{2} \cdot \cos(45^\circ) = \frac{F}{2\sqrt{2}} \)
- \( F_{ACy} = \frac{F}{2} \cdot \sin(45^\circ) = \frac{F}{2\sqrt{2}} \)

Step 6: Calculate the Net Force Components
Now, we can sum the components:
- In the x-direction:
\( F_{net x} = F + \frac{F}{2\sqrt{2}} \)
- In the y-direction:
\( F_{net y} = F + \frac{F}{2\sqrt{2}} \)

Step 7: Calculate the Magnitude of the Net Force
The magnitude of the net force \( F_{net} \) can be calculated using the Pythagorean theorem:
\( F_{net} = \sqrt{(F + \frac{F}{2\sqrt{2}})^2 + (F + \frac{F}{2\sqrt{2}})^2} \)

Step 8: Simplify the Expression
This simplifies to:
\( F_{net} = \sqrt{2 \left(F + \frac{F}{2\sqrt{2}}\right)^2} \)
\( F_{net} = \sqrt{2} \left(F + \frac{F}{2\sqrt{2}}\right) \)

Final Result
Thus, the magnitude of the net force on any particle is:
\( F_{net} = F \left( \sqrt{2} + \frac{1}{\sqrt{2}} \right) = F \left( \frac{3}{\sqrt{2}} \right) \)