There is a conducting rod of length 2L that lies along x-axis from x=−L→x=L. If rod moves with velocityv=v0ˆi in the magnetic field→B=B0ˆk, then induced EMF between ends of rod is
Zero
23B0Lv0
13B0Lv0
2B0Lv0
To find the induced EMF between the ends of the conducting rod, we can use the formula for induced EMF (ε) in a moving conductor in a magnetic field, which is given by:
ε=L⋅(v×B)
where:
- L is the length of the rod,
- v is the velocity of the rod,
- B is the magnetic field.
Step 1: Identify the parameters
The rod has a length of 2L and is oriented along the x-axis from x=−L to x=L. The velocity of the rod is given as →v=v0^i (along the x-axis), and the magnetic field is →B=B0^k (along the z-axis).
Step 2: Calculate the cross product v×B
To find the induced EMF, we first need to calculate the cross product →v×→B:
→v×→B=(v0^i)×(B0^k)
Using the right-hand rule and the properties of cross products, we can determine that:
^i×^k=^j
Thus, we have:
→v×→B=v0B0^j
Step 3: Substitute into the EMF formula
Now, we substitute this result into the EMF formula:
ε=L⋅(v0B0^j)
Since the length of the rod is 2L, we can write:
ε=2L⋅(v0B0^j)
Step 4: Determine the direction of the EMF
The induced EMF will be in the direction of ^j, which is perpendicular to both the velocity and the magnetic field.
Final Result
Thus, the induced EMF between the ends of the rod is:
ε=2Lv0B0
- L is the length of the rod,
- v is the velocity of the rod,
- B is the magnetic field.
The rod has a length of 2L and is oriented along the x-axis from x=−L to x=L. The velocity of the rod is given as →v=v0^i (along the x-axis), and the magnetic field is →B=B0^k (along the z-axis).
To find the induced EMF, we first need to calculate the cross product →v×→B:
Now, we substitute this result into the EMF formula:
The induced EMF will be in the direction of ^j, which is perpendicular to both the velocity and the magnetic field.
Thus, the induced EMF between the ends of the rod is:
Topper's Solved these Questions
Similar Questions
The magnetic field inn a region is given by →B=→kB0LywhereLisafixed≤n>h.Aconduct∈grodof≤n>hLliesalongtheY−aξsbetweentheorig∈andthep∮(0,L,0).Iftherodmoveswithavelocityv= v_0 veci, find the emf induced between the ends of the rod.
View SolutionThe magnetic field in a region is given by →B=B0Lxˆk where L is a fixed length.A conducting rod of length lies along the X-axis between the origin and the point (L,0,0).If the rod moves with a velocity →v=v0ˆj the emf induced between the ends of the rod.
View Solution
Knowledge Check
A metal rod of length I is moved with velocity v in a uniform magnetic field →B. Emf is induced between the two ends of rod
Awhen →l is parallel to →BBwhen →l is parallel to →vCwhen →v is parallel to →BDnone of the above casesA conductor PQ , with PQ=r , moves with a velocity v in a uniform magnetic field of induced B . The emf induced in the rod is
A(→v×→B).→rB→v.(→r×→B)C→B.(→r×→v)D∣∣→r×(→v×→B)∣∣
A glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA square loop of side d is moved with velocity vˆi in an non-uniform magnetic field B0axˆk then the emf induced shown is?
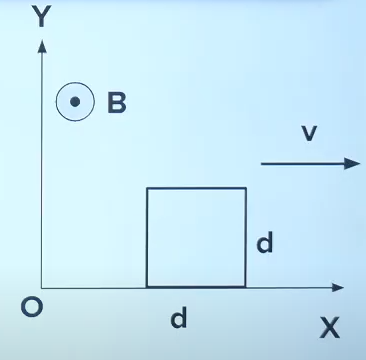
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA thin conducting rod of length l=5m is moved such that its end B moves along the X-axis while end A moves along the Y-axis A uniform magnetic field B=6ˆk T exists

View SolutionA conducting rod of length l is kept parallel to a uniform magnetic field →B. It is moved along the magnetic field with a velocity →v. What is the value of emf induced in the conductor?
View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)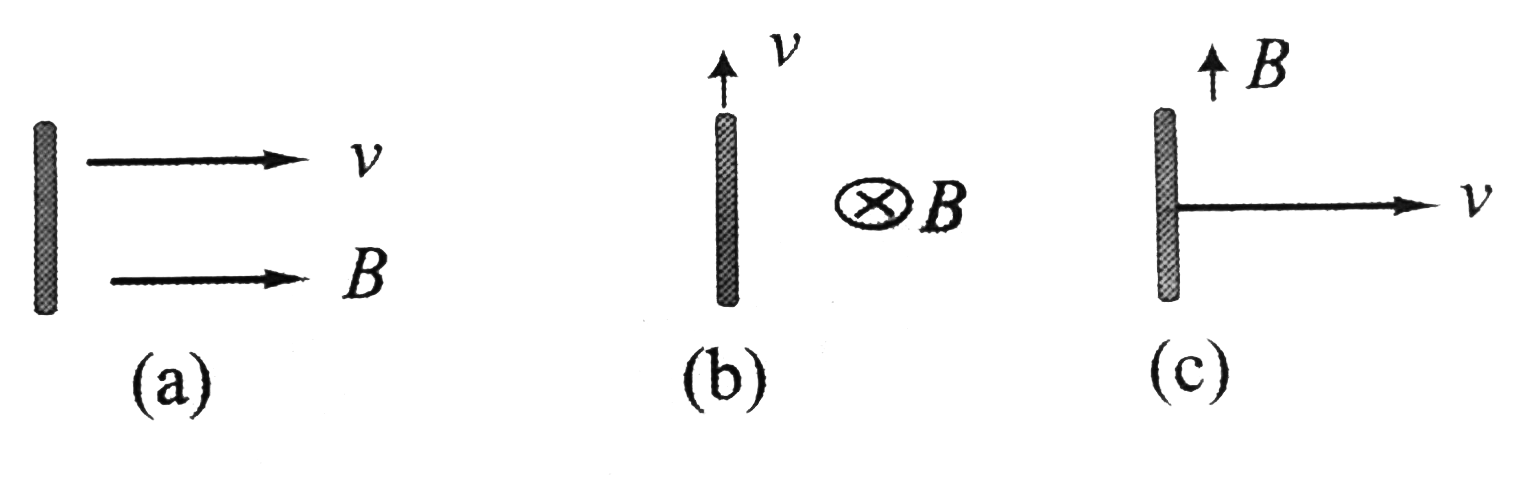
View Solution
