In a series LCR, AC circuit, if VL=800, VC=1600Vand applied voltage is 1000V, then power factor is
0.6
0.8
1
Zero
To find the power factor in a series LCR AC circuit, we can follow these steps:
Step 1: Identify the Given Values
- Voltage across the inductor, VL=800V
- Voltage across the capacitor, VC=1600V
- Applied voltage, V=1000V
Step 2: Calculate the Voltage Difference
The difference between the voltages across the inductor and capacitor is given by:
VL−C=VL−VC=800V−1600V=−800V
(Note: The negative sign indicates that the voltage across the capacitor is greater than that across the inductor.)
Step 3: Calculate the Reactive Voltage
The reactive voltage can be expressed as:
VR=√V2−(VL−VC)2
Substituting the known values:
VR=√(1000)2−(−800)2
Calculating the squares:
VR=√1000000−640000=√360000=600V
Step 4: Calculate the Tangent of the Phase Angle
The tangent of the phase angle ϕ can be calculated using the formula:
tanϕ=VL−VCVR
Substituting the values:
tanϕ=−800600=−43
Step 5: Calculate the Cosine of the Phase Angle
To find the power factor, we need to find cosϕ. We can use the identity:
cos2ϕ+sin2ϕ=1
From the tangent, we can find sinϕ and cosϕ:
- Let sinϕ=45 (from the triangle formed by the opposite side being 4 and adjacent side being 3)
- Let cosϕ=35
Step 6: Calculate the Power Factor
The power factor is given by:
Power Factor=cosϕ=35=0.6
Final Answer
Thus, the power factor of the circuit is:
Power Factor=0.6
---
- Voltage across the inductor, VL=800V
- Voltage across the capacitor, VC=1600V
- Applied voltage, V=1000V
The difference between the voltages across the inductor and capacitor is given by:
VL−C=VL−VC=800V−1600V=−800V
(Note: The negative sign indicates that the voltage across the capacitor is greater than that across the inductor.)
The reactive voltage can be expressed as:
VR=√V2−(VL−VC)2
Substituting the known values:
VR=√(1000)2−(−800)2
Calculating the squares:
VR=√1000000−640000=√360000=600V
The tangent of the phase angle ϕ can be calculated using the formula:
tanϕ=VL−VCVR
Substituting the values:
tanϕ=−800600=−43
To find the power factor, we need to find cosϕ. We can use the identity:
cos2ϕ+sin2ϕ=1
From the tangent, we can find sinϕ and cosϕ:
- Let sinϕ=45 (from the triangle formed by the opposite side being 4 and adjacent side being 3)
- Let cosϕ=35
The power factor is given by:
Power Factor=cosϕ=35=0.6
Thus, the power factor of the circuit is:
Power Factor=0.6
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
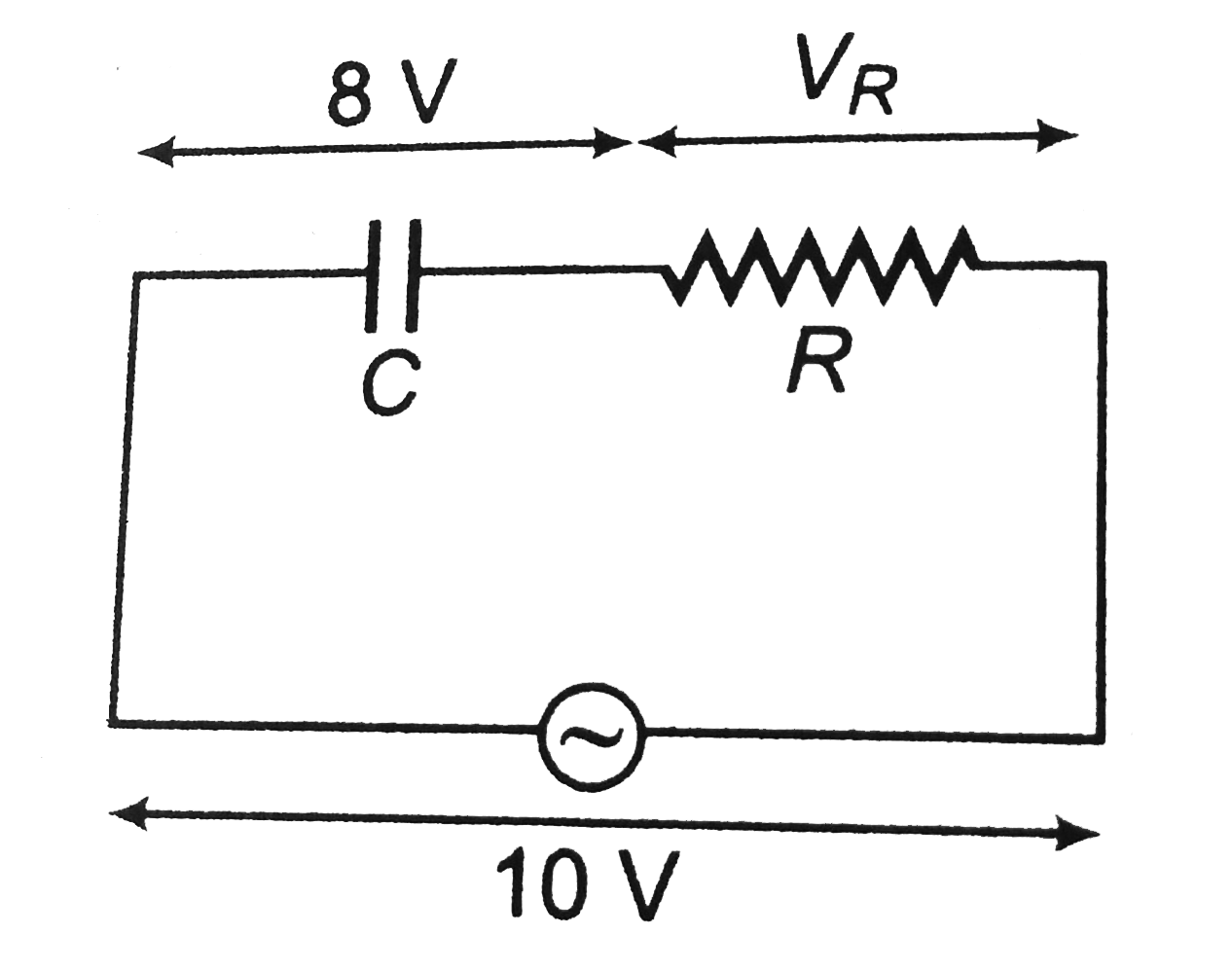 .A6V,tan−1(43)B3V,tan−1(34)C6V,tan−1(34)Dnone of these
.A6V,tan−1(43)B3V,tan−1(34)C6V,tan−1(34)Dnone of theseIn a series L−C−R circuit, currenrt in the circuit is 11A when the applied voltage is 220V. voltage across the caspcitor is 200V. If the value of resistor is 20Ω, then the voltage across the unknown inductor is
AzeroB200VC20VDnone of theseIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
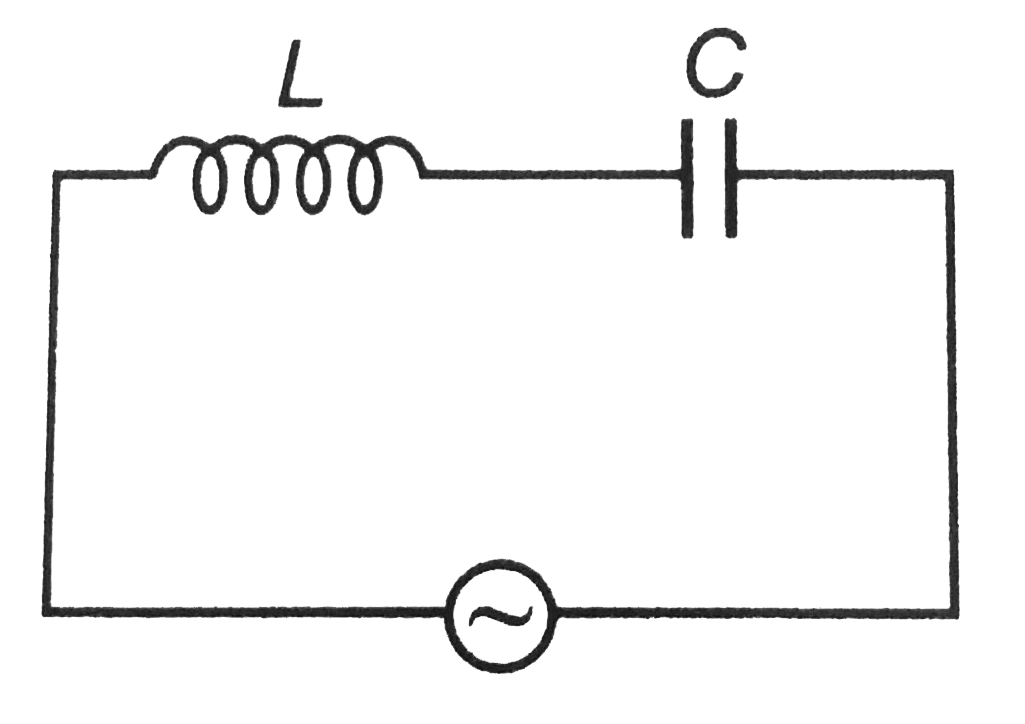 .AVL=V02,VC=V02BVL=0,VC=V0CVL=V0,VC=0DVL=−VC=V02
.AVL=V02,VC=V02BVL=0,VC=V0CVL=V0,VC=0DVL=−VC=V02
(a) Explain the term ' Sharpness of resonance' in ac circuit. (b) In a series LCR circuit , VL=VC≠VR. What is the value of power factor for this circuit?
View SolutionIn a series LCR circuit, VL=VC≠VR. What is the value of power factor ?
View SolutionStatement 1: In a series RLC circuit if (VR),(VL)and(VC) denote rms voltage across R,L and C respectively and (VS) is the rms voltage across the source. Then (Vs)=(VR)+(VL)+(VC)
Statement 2: In ac circuit, Kirchhoff's voltage law is correct at every instant of same.

View SolutionIn an AC circuit , current is 3A and voltage 210V and power is 63W. The power factor is
View SolutionIn an L-C-R circuit, if V is the effective value of the applied voltage VR is the voltage across R, VL is the effective voltage across L, VC is the effective voltage across C, then
View Solution