An element of length →Δl=ΔzˆK is placed at origin and carries a large current l=15A. The magnetic field on the y axis at a distance of 0.75 m is (Δz=0.75cm)
2×10−8 T along negative x-axis
2×10−8T along positive x-axis
Zero
2×10−8T along negative y-axis
To solve the problem, we will use the Biot-Savart Law, which gives the magnetic field →B produced at a point in space by a current-carrying conductor. The law states:
d→B=μ04πId→l×→rr3
Where:
- d→B is the magnetic field contribution from the current element,
- μ0 is the permeability of free space,
- I is the current,
- d→l is the differential length vector,
- →r is the position vector from the current element to the point where the field is being calculated,
- r is the magnitude of →r.
1. Identify the Current Element and Position Vector:
- The current element is along the z-axis, so d→l=d→z^k.
- The current I=15A.
- We are calculating the magnetic field at a point on the y-axis at a distance 0.75m (which is 75cm) from the origin. Therefore, the position vector →r from the current element to the point on the y-axis is →r=0^i+0.75^j+0^k.
2. Calculate the Magnitude of →r:
- The magnitude r=|→r|=√02+(0.75)2+02=0.75m.
3. Cross Product Calculation:
- We need to compute d→l×→r:
d→l=d→z^kand→r=0^i+0.75^j+0^k
- The cross product d→l×→r is:
d→l×→r=^k×(0.75^j)=−0.75^i
4. Substituting into Biot-Savart Law:
- Substitute d→B into the Biot-Savart Law:
d→B=μ04πI(−0.75^i)(0.75)3
- Calculate (0.75)3=0.421875.
5. Final Calculation:
- Now substituting I=15:
d→B=μ04π15×(−0.75^i)0.421875
- Simplifying:
d→B=μ0⋅15⋅(−0.75)4π⋅0.421875^i
6. Direction of the Magnetic Field:
- The direction of the magnetic field is in the negative x-direction, which can be represented as −^i.
Final Answer:
The magnetic field at the point on the y-axis at a distance of 0.75 m from the origin is directed along the negative x-axis.
- d→B is the magnetic field contribution from the current element,
- μ0 is the permeability of free space,
- I is the current,
- d→l is the differential length vector,
- →r is the position vector from the current element to the point where the field is being calculated,
- r is the magnitude of →r.
- The current element is along the z-axis, so d→l=d→z^k.
- The current I=15A.
- We are calculating the magnetic field at a point on the y-axis at a distance 0.75m (which is 75cm) from the origin. Therefore, the position vector →r from the current element to the point on the y-axis is →r=0^i+0.75^j+0^k.
- The magnitude r=|→r|=√02+(0.75)2+02=0.75m.
- We need to compute d→l×→r:
d→l=d→z^kand→r=0^i+0.75^j+0^k
- The cross product d→l×→r is:
d→l×→r=^k×(0.75^j)=−0.75^i
- Substitute d→B into the Biot-Savart Law:
d→B=μ04πI(−0.75^i)(0.75)3
- Calculate (0.75)3=0.421875.
- Now substituting I=15:
d→B=μ04π15×(−0.75^i)0.421875
- Simplifying:
d→B=μ0⋅15⋅(−0.75)4π⋅0.421875^i
- The direction of the magnetic field is in the negative x-direction, which can be represented as −^i.
The magnetic field at the point on the y-axis at a distance of 0.75 m from the origin is directed along the negative x-axis.
Topper's Solved these Questions
Similar Questions
An element of length −→Δl=Δzˆk is placed at origin and carries a large current l=15 A.The magnetic field on the y-axis at a distance of 0.75 m is (Δz=0.75 cm)
View SolutionAn element d→l=dxˆi (where dx=1cm) is placed at the origin and carries a large current i=10A. What is the magnetic field on the Y-axis at a distance of 0.5m?
View Solution
Knowledge Check
An element d→l=dxˆi (where dx=1cm) is placed at the origin and carries a large current i=10A. What is the magnetic field on the Y-axis at a distance of 0.5m?
A2×108TB4×108TC6×108TD8×108TA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)A2×10−4wb/m2B3×10−5Wb/m2C4×10−4Wb/m2D4×10−5Wb/m2
An element d→l=dxˆi (where dx=1cm) is placed at the origin and carries a large current i=10A. What is the magnetic field on the Y-axis at a distance of 0.5m?
View SolutionAn element, Δ→t=Δxˆi is placed at the origin as shown in figure and carries a current 5A. Find out the magnetic field at point P on the z-axis at a distance of 2−0m due to the element Δx=1cm. Give also, the direction of the magnetic field produced.

View SolutionAn element Δ→l=Δxˆi is placed at the origin as shown in figure and carries a current I=2A. Find out the magnetic field at a point P on the y-axis at a distance of 1⋅0m due to the element Δx=1cm. Give also the direction of the field produced.
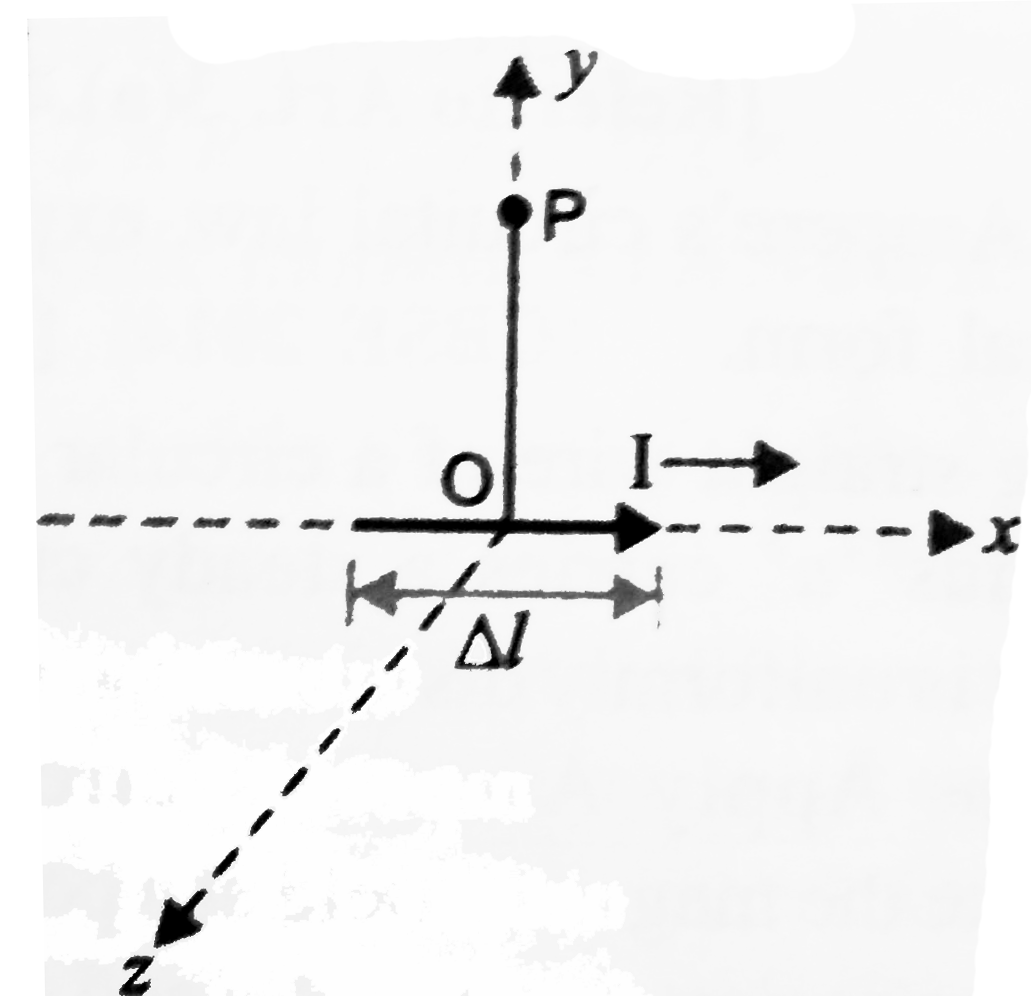
View SolutionAn element →Δ=Δxˆi is placed at the origin as shown (fig.) and carries a current I = 2 A . Find out the magnetic field at a point p on the y-axis at a distance of 1.0 m due to the element Δx=1cm. Give the direction of the field produced.
View SolutionAn element of 0.05ˆim is placed at the origin as shown in figure which carries a large current of 10 A. The magnetic field at a distance of 1 m in perpendicular direction is

View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View Solution
