Displacement current can be expressed as (symbols have their usual meanings)
(μ0ε0)(dϕEdt)
(1μ0ε0)(dϕEdt)
(ε0)(dϕEdt)
(μ0)(dϕEdt)
To express the displacement current, we can follow these steps:
Step 1: Understanding the Concept of Displacement Current
Displacement current is a term introduced by James Clerk Maxwell to account for changing electric fields in situations where there is no actual current flowing. It is particularly important in the context of electromagnetic waves and in capacitors where the electric field changes over time.
Step 2: Maxwell's Modification of Ampere's Law
Maxwell modified Ampere's Law to include the displacement current. The original form of Ampere's Law states that the line integral of the magnetic field B around a closed loop is proportional to the total current I passing through the loop:
∮B⋅dl=μ0I
where μ0 is the permeability of free space.
Step 3: Introducing Displacement Current
Maxwell introduced the concept of displacement current Id to account for the changing electric field in a capacitor. The modified equation becomes:
∮B⋅dl=μ0I+μ0Id
Step 4: Expression for Displacement Current
The displacement current Id is defined in terms of the rate of change of the electric field E over time. It is given by:
Id=ϵ0dΦEdt
where ΦE is the electric flux given by ΦE=∫E⋅dA and ϵ0 is the permittivity of free space.
Step 5: Final Expression
Thus, the displacement current can be expressed as:
Id=ϵ0dEdt
This expression shows that the displacement current is proportional to the rate of change of the electric field.
Displacement current is a term introduced by James Clerk Maxwell to account for changing electric fields in situations where there is no actual current flowing. It is particularly important in the context of electromagnetic waves and in capacitors where the electric field changes over time.
Maxwell modified Ampere's Law to include the displacement current. The original form of Ampere's Law states that the line integral of the magnetic field B around a closed loop is proportional to the total current I passing through the loop:
Maxwell introduced the concept of displacement current Id to account for the changing electric field in a capacitor. The modified equation becomes:
The displacement current Id is defined in terms of the rate of change of the electric field E over time. It is given by:
Thus, the displacement current can be expressed as:
Topper's Solved these Questions
Similar Questions
Knowledge Check
The correct form of Stroke's law is (symbols have their usual meanings)
A→F=−6πηa→vB→F=6πηa→vC→F=−4πηa→vD→F=4πηa→vThe correct combination is (symbols have their usual meanings)
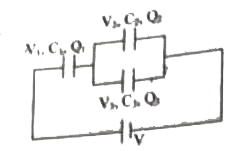 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3Bohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πme
Select the incorrect relation. (Where symboles have their usual meanings):-
View SolutionChoose the correct arrangement. The symbols have their usual meanings
View SolutionChoose the correct arrangement, where the symbols have their usual meanings
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionIn mu-particle scattering experiment, the expression of distance of closest approach (r0)is (symbols have their usual meanings)
View Solution
