The position of S.H.M. is given by x=2[√3sinπt+cosπt]. The amplitude of motion is [ x is in metre and symbols have the usual meaning]
2m
4m
1m
√3 m
To find the amplitude of the simple harmonic motion (S.H.M.) given by the equation x=2(√3sin(πt)+cos(πt)), we can follow these steps:
Step 1: Rewrite the equation
We start with the given equation:
x=2(√3sin(πt)+cos(πt))
Step 2: Factor out the constant
We can factor out the 2:
x=2√3sin(πt)+2cos(πt)
Step 3: Combine the sine and cosine terms
We can express the combination of sine and cosine in the form of Rsin(πt+ϕ), where R is the amplitude and ϕ is the phase angle.
To do this, we find R using the formula:
R=√(2√3)2+(2)2
Step 4: Calculate R
Calculating R:
R=√(2√3)2+(2)2=√4⋅3+4=√12+4=√16=4
Step 5: Conclusion
The amplitude of the motion is R=4 meters.
Thus, the final answer is:
Amplitude=4 meters
---
We start with the given equation:
x=2(√3sin(πt)+cos(πt))
We can factor out the 2:
x=2√3sin(πt)+2cos(πt)
We can express the combination of sine and cosine in the form of Rsin(πt+ϕ), where R is the amplitude and ϕ is the phase angle.
R=√(2√3)2+(2)2
Calculating R:
R=√(2√3)2+(2)2=√4⋅3+4=√12+4=√16=4
The amplitude of the motion is R=4 meters.
Amplitude=4 meters
Topper's Solved these Questions
Similar Questions
Knowledge Check
The pressure exerted by a liquid of height h is given by(symbols have their usuall meanings)
AhdgBhdgChdDh gAn SHM is give by y=5[sin(3πt)+√3cos(3πt)]. What is the amplitude of the motion of y in metre ?
A10B20C1D5A S.H.M. is represented by x=5√2(sin2πt+cos2πt) amplitude of the S.H. M is
A10 cmB20 cmC5√2D50 cm
The differnetial equation of S.H.M is given by d2xdt2+∝x=0. The frequency of motion is
View SolutionIf H=1√3V, then find angle of dip. (where symbols have their usual meaning)
View SolutionThe displacement of a particle in S.H.M. is given by x=5[cosπt+sinπt] where x is in metre. The amplitude of motion of the particle is given by
View SolutionThe S.H.M. of a particle is given by the equation y=3sinωt+4cosωt . The amplitude is
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
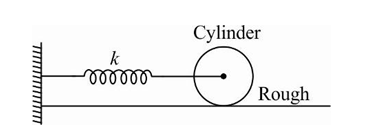
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:
View Solution
