A wire of length 1m along x-axis carries a current 2A , is placed inside the field of →B=(3.0ˆj+4.0ˆk) tesla, then force exerted on the wire is
6ˆk+8ˆj
6ˆk−8ˆj
8ˆk−6ˆj
8ˆk−6ˆj
To find the force exerted on the wire, we can use the formula for the magnetic force on a current-carrying wire, which is given by:
→F=I→L×→B
where:
- →F is the force vector,
- I is the current in the wire,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
1. Identify the Given Values:
- Length of the wire L=1m
- Current I=2A
- Magnetic field →B=3^j+4^kT
2. Define the Length Vector:
Since the wire is along the x-axis, we can express the length vector as:
→L=1^im
3. Calculate the Cross Product:
We need to calculate →L×→B:
→L×→B=(1^i)×(3^j+4^k)
Using the distributive property of the cross product:
→L×→B=1^i×3^j+1^i×4^k
Now, calculate each term:
- ^i×^j=^k
- ^i×^k=−^j
Therefore:
→L×→B=3^k−4^j
4. Multiply by the Current:
Now, multiply the result by the current I:
→F=I(→L×→B)=2(3^k−4^j)
This gives:
→F=6^k−8^j
5. Final Result:
The force exerted on the wire is:
→F=−8^j+6^kN
- →F is the force vector,
- I is the current in the wire,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
- Length of the wire L=1m
- Current I=2A
- Magnetic field →B=3^j+4^kT
Since the wire is along the x-axis, we can express the length vector as:
→L=1^im
We need to calculate →L×→B:
→L×→B=(1^i)×(3^j+4^k)
Using the distributive property of the cross product:
→L×→B=1^i×3^j+1^i×4^k
- ^i×^j=^k
- ^i×^k=−^j
→L×→B=3^k−4^j
Now, multiply the result by the current I:
→F=I(→L×→B)=2(3^k−4^j)
This gives:
→F=6^k−8^j
The force exerted on the wire is:
→F=−8^j+6^kN
Topper's Solved these Questions
Similar Questions
A wire of length l metre carries a current I ampere along the Y-axis. A magnetic field, →B=B0(ˆi+ˆj+ˆk) tesla exists in space. Find the magnitude of the force on the wire.
View SolutionA straight wire of1.4 m long carries a current of 7 A at right angles to a uniform magnetic field of 0.01 T. Calculate the mechanical force acting on the wire due to the magnetic field.
View Solution
Knowledge Check
A straight wire of length 1 m, and carrying a current of 1.8 A, is placed in a uniform magnetic field of induction 2T. If the magntic field is perpendicular to the length of the wire, then the force acting on the wire is
A1.8NB3.6NC0.9ND2.5NA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
A2.4NB1.2NC3.0ND2.0NA wire of length 1 m placed in x-z plane carries current of 1 amp. The coefficient of friction between wire and the surface is 0.2 and mass of the wire is 2. The magnetic field of strengh 2 T exists along position y direction . Then choose the correct statment .
AAcceleration of wire is 0.5m/s2BWire will not move at allCAccceleration of wire is m/s2DAcceleration of wire is 2m/s2
A wire of iength I carries a current along the x-axis. A magnetic field B=B0(ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire of length a'a carries a current I along the y-axis.A magnetic field exists given by
B=B0(3ˆi+2ˆj+ˆk)T
Calculate magnetic force in vector from and its magnitude
View SolutionA magnetic field →B=(ˆi+0.5ˆj+0.25ˆk) T exists in a space. A wire of length →l=(0.25ˆi−0.25ˆj) m carries a current of 1 A and is placed in the magnetic field region.
Find the magnitude of magnetic force on the wire.
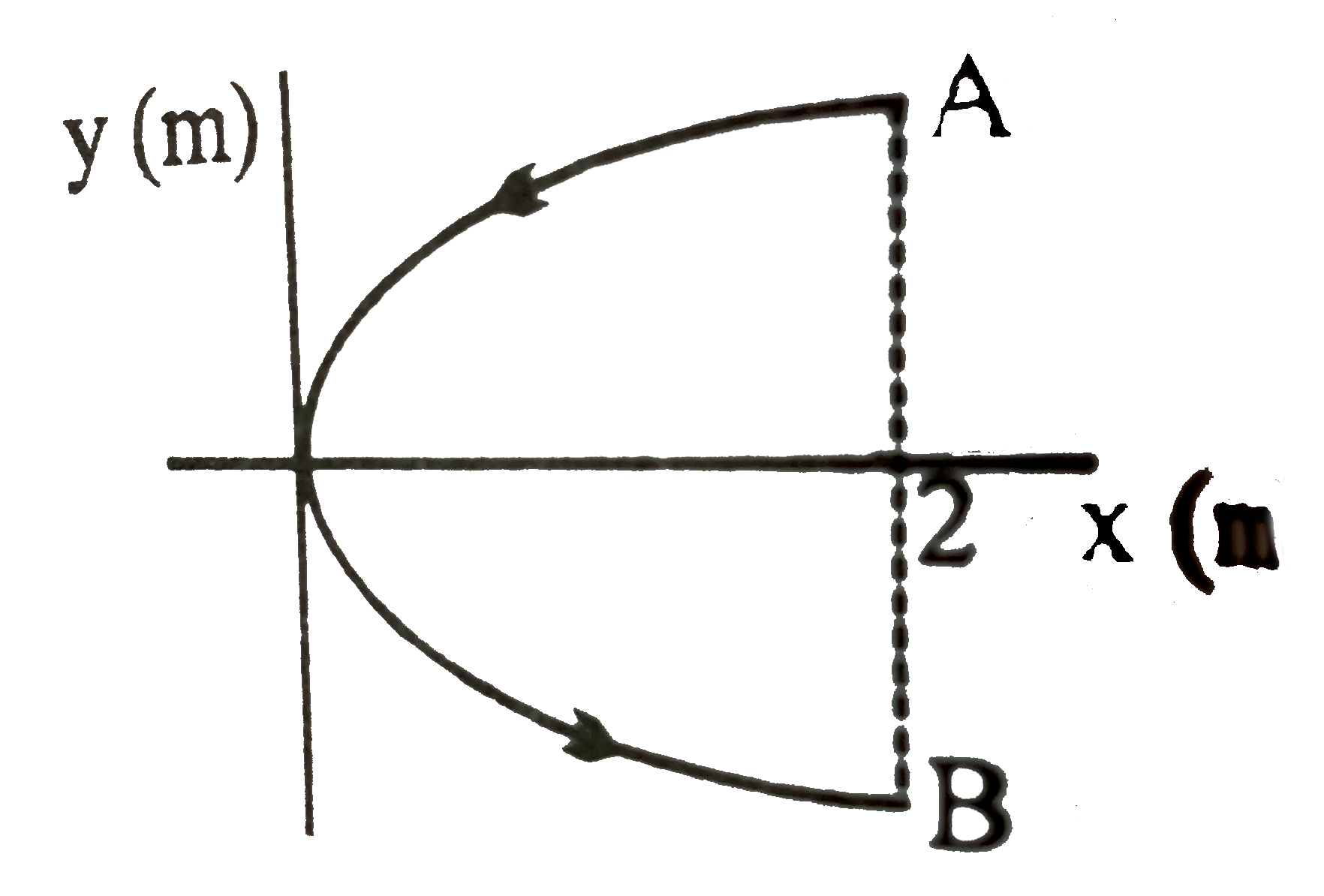
View SolutionA conducting wire bent in the from of a parabola y2=2x carries a current i=2A as shown in figure This wire is placed in a unifrom magnetic field
→B=−4ˆk Tesla The magnetic force on the wire is (newton)
 .
.
View SolutionA wire bent in the form a right angled triangle PQR, carries a current 1A. It is placed in a region of a uniform magnetic field B=0.2T. If PR=1m, the net force on the wire is

View Solution
