If y=log(1x) , show that dydx+ey=0Solution in Malayalam
Step by step video & image solution for If y=log(1/x) , show that dy/dx+e^y=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
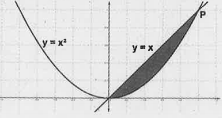
Consider the following figure
find the point of intersection (P) of the parabola and the line.
 03:37View Solution
03:37View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)03:46View SolutionIf xy=ex−y, show that dydx=logx{log(xe)}2
03:43View SolutionIf x^(y)=e^(x-y), then show that (dy)/(dx)=(log x)/((1+log x)^(2))
01:24View SolutionIf yx=ey−x , prove that dydx=(1+logy)2logy
01:21View SolutionIf y=eax Show that xdydx=ylogy.
04:43View SolutionIf y= elog(logx),thendydx =
View SolutionIf x log xdydx+y=logx2 and y(e)=0 , then
y(e2)=06:47View SolutionIf xlogxdydx+y=logx2andy(e)=0, then y(e2)=
02:16View SolutionIf y=exex...∞,show that,dydx=y2logyx(1−ylogxlogy).
03:49View SolutionIf y=e[log(x+1)−logx]. Finddydx
03:54View SolutionIf xy=ex−y, show that dydx=logx{log(xe)}2
02:28View SolutionFind dydx:
x=ecos2tandy=esin2t show that, dydx=−ylogxxlogy02:37View SolutionIf y=elogx, show that dydx=1
02:07View SolutionIf xy=ex−y, then show that dydx=logx(1+logx)2
04:36View Solution

