यदि y=axax....∞ हो, तो सिद्ध कीजिए कि dydx=y2logeyx(1−ylogelogey)
Step by step video & image solution for यदि y =a ^(x ^(a ^(x^(.^(.^(.^(.^(oo)))))))) हो, तो सिद्ध कीजिए कि (dy)/(dx) = (y ^(2) log _(e) y )/( x (1- y log _(e) log _(e) y )) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
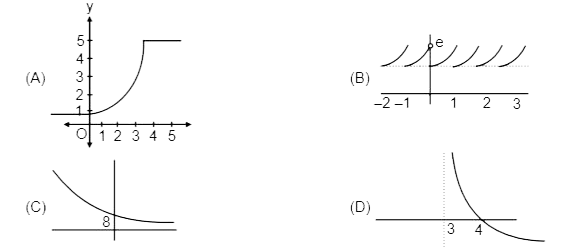
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
View SolutionIf yx=ey−x, prove that dydx=(1+logy)2logy
View SolutionIf yx=ey−x , prove that dydx=(1+logy)2logy
View SolutionIf x=ecos2t and y=esin2t , prove that dydx=−ylogxxlogy
View SolutionIf ln(ln x-ln y)=e^(x^(2)y)(1-ln x) , then y'(e) equals
View Solutionयदि yy=ex−y तो सिद्ध कीजिये कि dydx=log x(1+logx)2
View SolutionIf y= elog(logx),thendydx =
View SolutionIf yx=ey−x, prove that dydx=(1+logy)2logy.
View Solutionयदि xy=ey−x, तो सिध्द कीजिए कि dydx=2−logx(1−logx)2
View Solutionयदि y=x logxa+bx हो, तो सिध्द कीजिए कि x3d2ydx2=(xdydx−y)2
View SolutionIf x log xdydx+y=logx2 and y(e)=0 , then
y(e2)=
View SolutionIf xlogxdydx+y=logx2andy(e)=0, then y(e2)=
View SolutionIf y=exex...∞,show that,dydx=y2logyx(1−ylogxlogy).
View SolutionIf yyy.,,∞=loge(x+loge(x+.....)), then dydxat(x=e2−2,y√2) is
View SolutionFind dydx:
x=ecos2tandy=esin2t show that, dydx=−ylogxxlogy
View Solution
