From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2 .
 Solution in Gujrati
Solution in Gujrati
Step by step video & image solution for From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm^(2) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - KUMAR PRAKASHANCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - KUMAR PRAKASHANCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.3
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - KUMAR PRAKASHANCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OTHER IMPORTANT EXAMPLES
11 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Objective Questions (True or false)
5 Videos
- TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - TRIANGLESEXERCISE - OBJECTIVE QUESTIONS
37 Videos
Similar Questions
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius find the volume of the solid in terms of π

View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. find the height of the cylinder.
View SolutionThe internal and external diameters of a hollow hemispherical veseel are 12 cm and 16 cm respectively. If the cost of painting 1cm2 of the surface area is Rs 5.00 find the total cost of painting the vessel all over. (Use π=3.14)

View SolutionFor any frequency distribution, mean is always greater than mode.
View SolutionFill in the blanks so as to make each of the following statements true :
ΔABC~ΔDEF and 2AB=DE. If BC= 8 cm, then EF=………cm.
View SolutionFrom a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Take π=22/7 )
View SolutionFrom a solid cylinder of height 36 cm and radius 14 cm a conical cavity of radus 7 cm and height 24 cm is drilled out . Find the volume and the total surface area of the remaining solid.
View SolutionMatch the following Column A to Column B

View SolutionFrom a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. [Useπ=3.14.]
View Solutionऊँचाई 2⋅4 सेमी और व्यास 1⋅4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है | शेष बचे ठोस का निकटतम वर्ग सेन्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
View Solutionएक ठोस बेलन, जिसकी ऊँचाई 2.4 सेमी तथा व्यास 1.4 सेमी है, में से उसी ऊँचाई तथा व्यास वाला एक शंकु खोदकर निकाल दिया गया है। शेष बचे ठोस का, निकटतम वर्ग सेमी तक कुल पृष्ठाय क्षेत्रफल ज्ञात कीजिए। [π=227का प्रयोग करें]
View Solutionऊचाई 12 cm और व्यास 10 cm वाले एक ठोस बेलन में से इसी ऊँचाई एवं व्यास बाला एक शंक्वाकार खोल (cavity) काट लिया जाता है । शेष बचे भाग का आयतन ज्ञात करें।
View Solutionएक 24 सेमी. ऊँचाई तथा 1.4 सेमी, व्यास वाले ठोस बेलन में से समान ऊँचाई और समान व्यास वाला एक शंकु के कार का खोल (cavity) काट लिया जाता है। शेष बचे हुए ठोस का पृष्टीय क्षेत्रफल निकटतम वर्ग सेमी, तक ज्ञात करें।
View SolutionFrom a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
View Solutionஉயரம் 2.4செ.மீ மற்றும் விட்டம் 1.4செ.மீ கொண்ட ஒரு திண்ம உருளையில் இருந்து அதேவிட்டமும் உயரமும் உள்ள ஒரு கூம்பு வெட்டி எடுக்கப்பட்டால் மீதமுள்ள திண்மத்தின் கனஅளவு எவ்வளவு கன செ.மீ ஆகும்? .
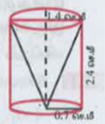
View SolutionThe height of a solid cylinder is 2.4 cm and the diameter is 1.4 cm. This caused the conical pits of the same height and diameter to be drilled and hollowed out. The total surface area of the new cube at a very close price cm^(2) Find out at
View Solution
