In ΔPQR,∠PQR=90∘andsegQS⊥ hypotenuse PR,-P-S-R,then Solution in Marathi
PR2=PQ×PR
QS2=PS×SR
PR2=PS×SR
QS2=PQ×QR
Step by step video & image solution for In DeltaPQR,anglePQR=90^(@) and seg QSbot hypotenuse PR,-P-S-R,then by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Aditional Problems for Practice(Based on the Practice Set 2.1)
15 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Aditional Problems for Practice(Based on the Practice Set 2.2)
4 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Activities for Practice
2 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Try This
1 Videos
- QUADRATIC EQUATIONSBOOK - TARGET PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Chapter Assessment
39 Videos
Similar Questions
Identify the Pythagorean triplets from the following:
i. (15,10,35)
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

View SolutionIn △ABC, point M is midpoint of side BC. If AB2+AC2=290cm2 and AM=8 cm, find BC.
View SolutionIn Which of the following experiments possibility of expected
outcome is more ?
(i) Getting I on the upper face when a die is thrown.
(ii) Getting head by tossing a coin.
View SolutionChoose the correct alternative.
(i) Which of the following is a quadratic equation?
View SolutionA ΔPQR , given that QR=3cm, ∠PQR=45∘ and QP−PR=2cm.
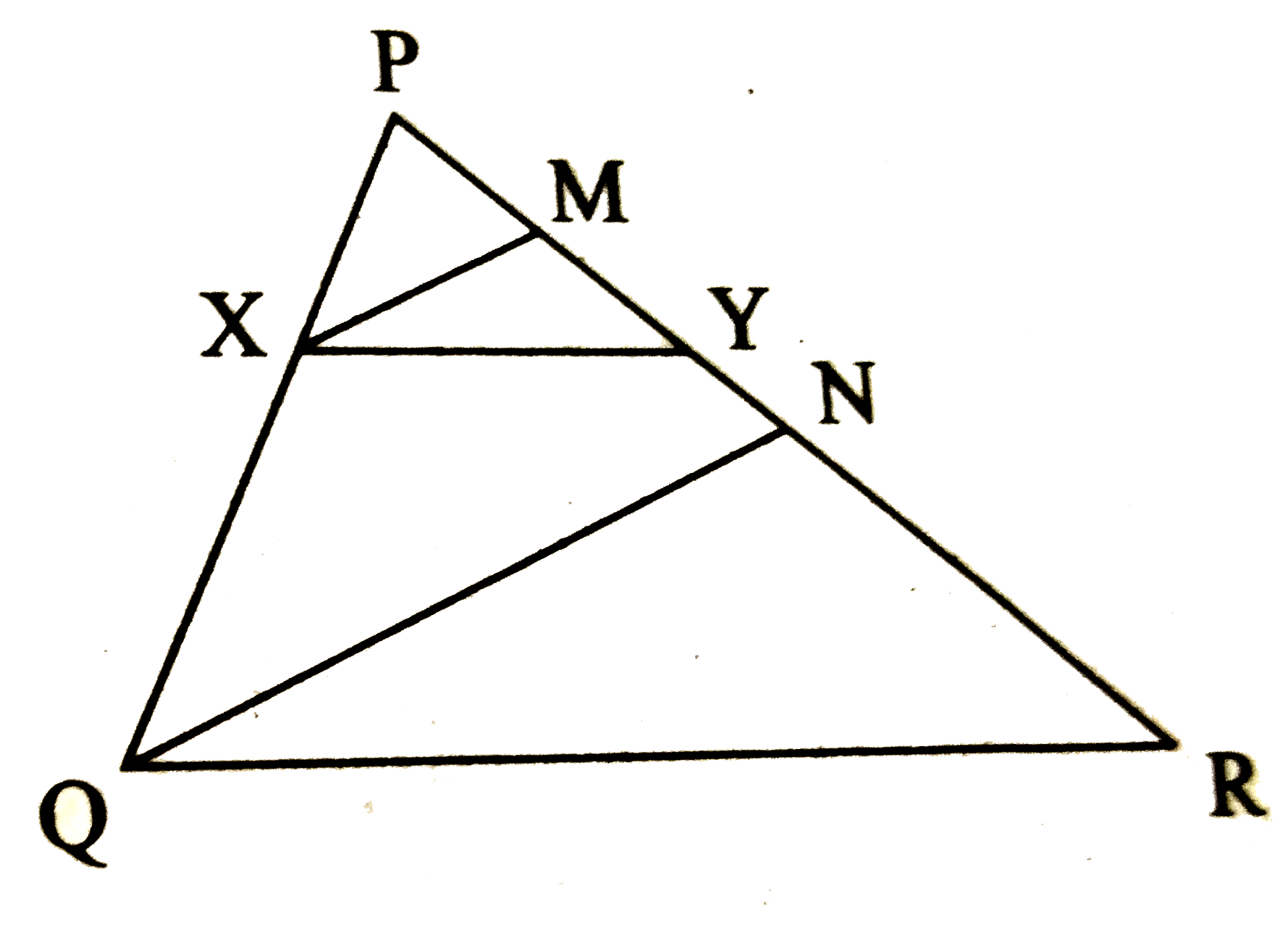
View SolutionIn ΔPQR, seg XY∣∣ side QR. M and N are the midpoints of seg PY and side PR respectively, P−M−Y−N−R.
Prove that (i)ΔPXM~ΔPQN
(ii) seg XM∣∣ seg QN.
View SolutionIn ΔPQR, ∠PQR=90∘, PQ=6 and QR=8 then the length of seg PR is……. .

View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn the figure, ∠LMN=∠LKN=90∘
seg MK⊥ seg LN.
Complete the following activity to prove R is the midpoint of seg MK.
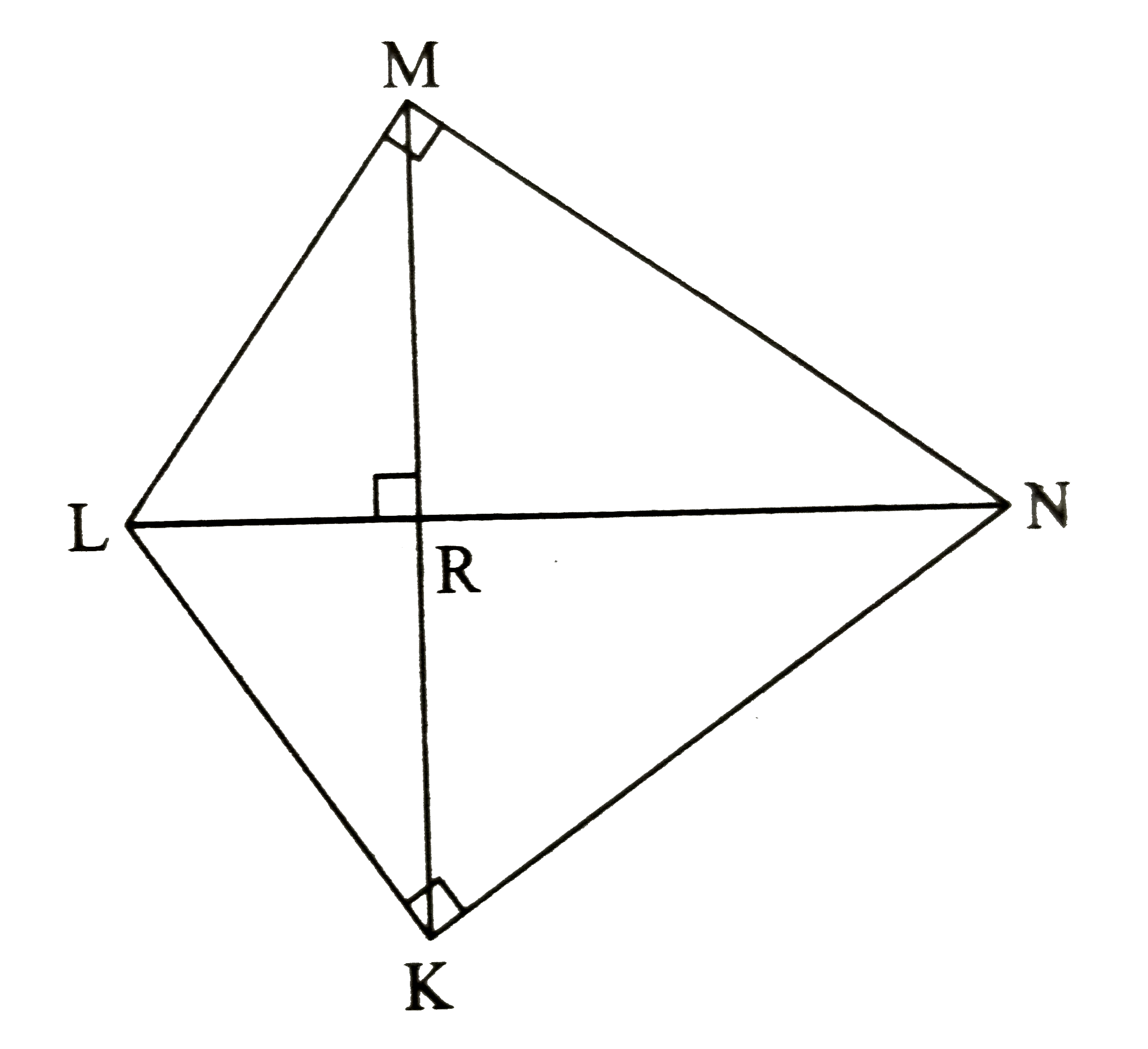
Proof: In ΔLMN, ∠LMN=90∘
seg MR⊥ hypotenuse LN
∴ by property of geometric mean,
MR2=□×RN
In ΔLKN, ∠LKN=90∘
seg KR⊥ hypotenuse LN
∴ by property of geometric mean,
KR2=LR×□
From (1) and (2), we get
MR2=□∴MR=□.
∴R is the midpoint of seg MK.
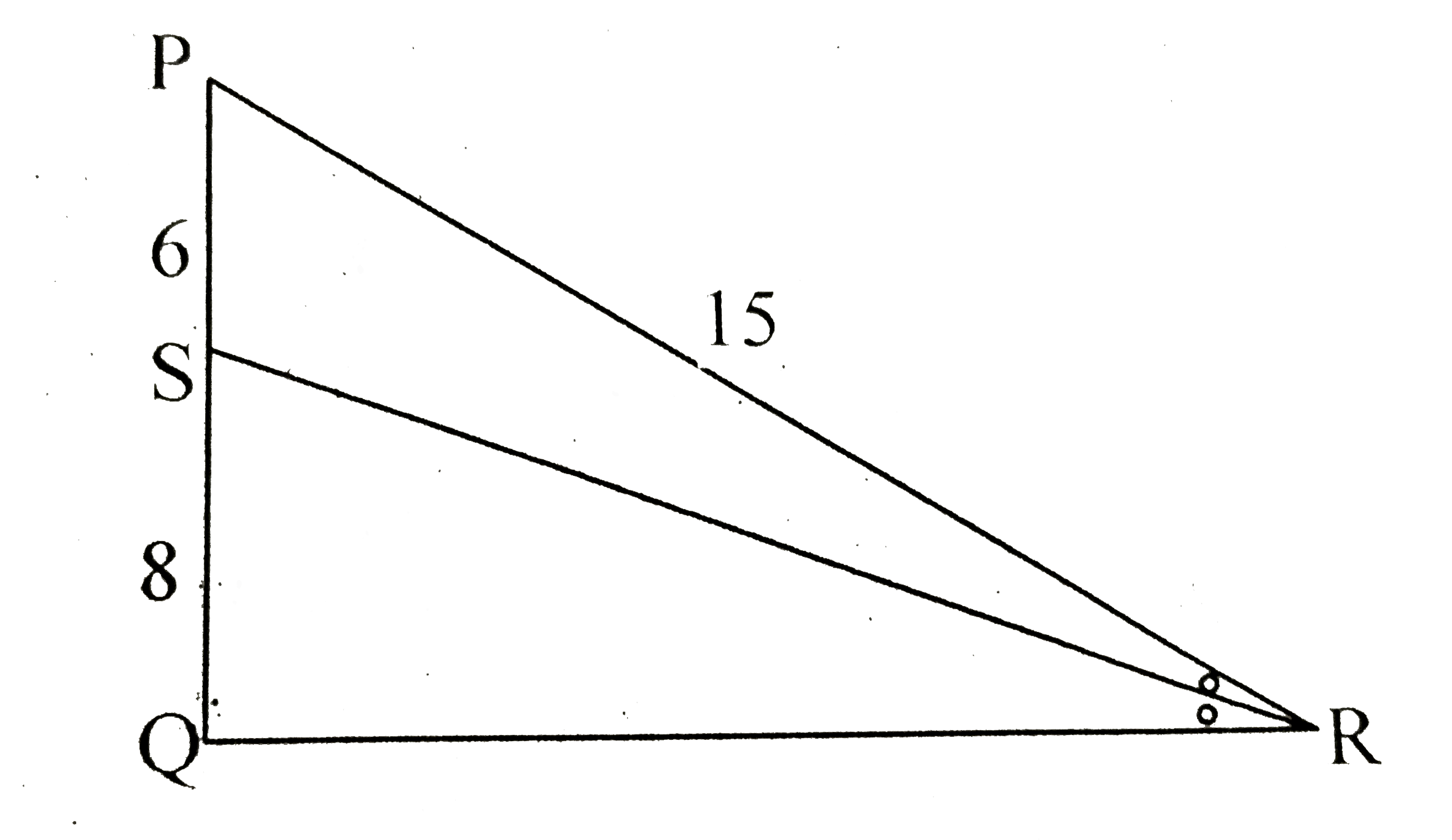
View SolutionIn the following figure, in ΔPQR, seg RS is the bisector of ∠PQR,PS=6,SQ=8,PR=15.
Find QR.
View SolutionIn ΔPQR seg RS is the bisector of ∠PQR,PS=8,SQ=6,PR=20 then QR = …………….
View SolutionIn ΔPQR,∠PQR=90∘, as show in figure, seg QS⊥sPR, seg QM is angle bisector of ∠PQR.
Prove that : PM2MR2=PSSR

View SolutionIn ΔPQR,∠PQR=90∘andsegQS⊥ hypotnuse PR,-P-S-R,then
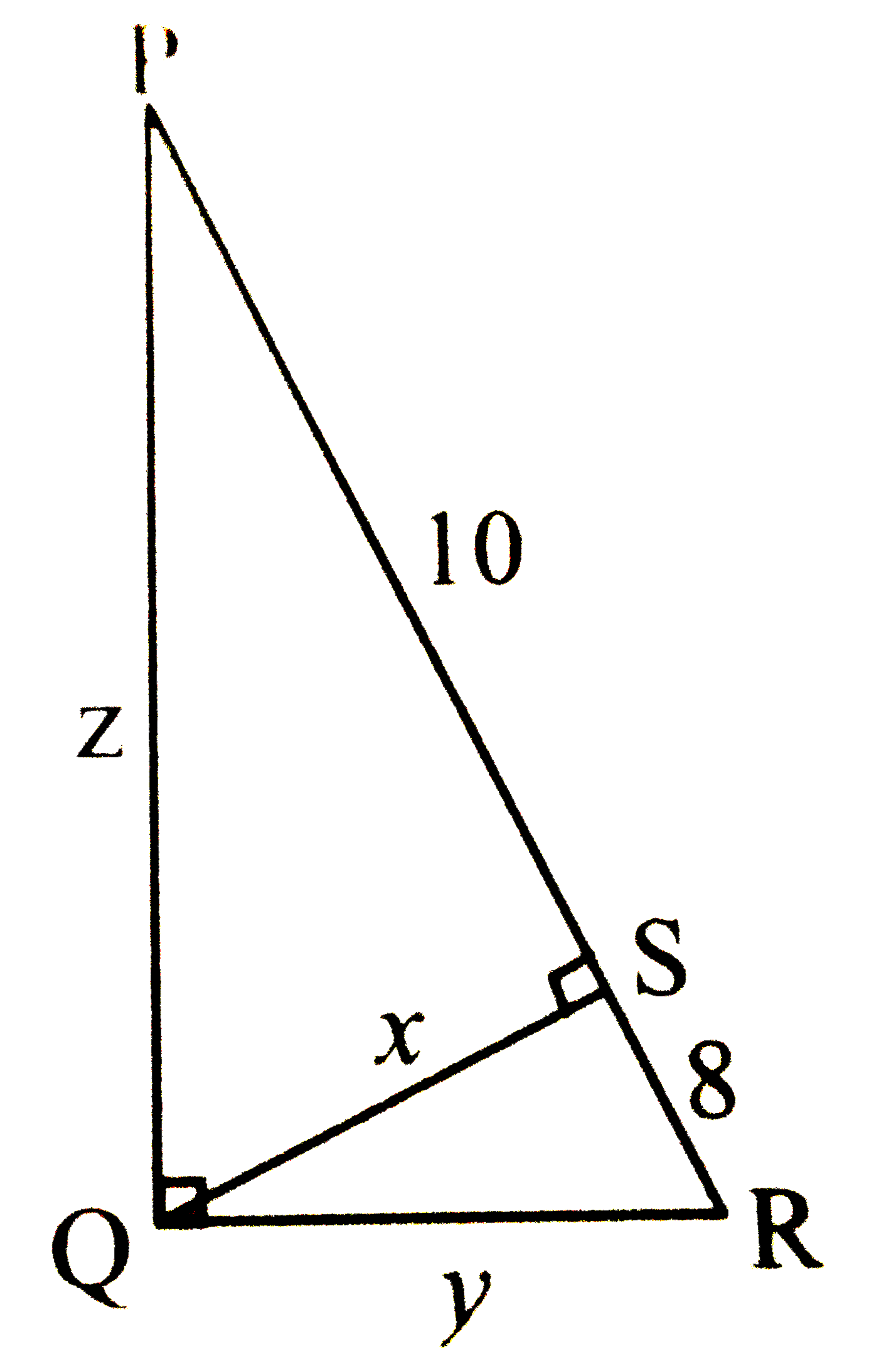
View SolutionSee the given figre. In ΔPQR,∠PQR=90∘, seg QS⊥ seg PR, then find x,y,z.
View Solution
