[A]: Dental formula is the number of teeth in upper jaws of one side and low jaw of same side
[B]: This can be used for non mammalian and insectivorous mammals also.
If both A and R are true and R is the correct explanation of A
If both A and R are true but R is not the correct explanation of A
If A is true and R is false
If both A and R are false
The correct Answer is:C
Step by step video & image solution for [A]: Dental formula is the number of teeth in upper jaws of one side and low jaw of same side [B]: This can be used for non mammalian and insectivorous mammals also. by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A hat contains a number of cards with 30% white on both sides, 50% black on one side and whit e on the other side, 20% black on both sides. The cards are mixed up, and a single card is drawn at random and placed on the table. Its upper side shows up black. The probability that its other side is also black is 2/9 b. 4/9 c. 2/3 d. 2/7
View SolutionInternal micrometer is a measuring intrument used to measure internal diameter (ID) of a large cylinder bore with high accuracy. Construction is shown in figure. There is one fixed rod B (to the right in figure) and one moved rod A (to the left in figure). It is based on the particle of advancement of a screw when it is rotated in a nut with internal threads. Main scale reading can be directly seen on the hub which is fixed with respect to rod B. When the cap is rotated rod A moves in or cut depending on direction of rotation. The circular scale reading is seen by checking which division of circular scale coincide with the references line
_E01_259_Q01.png)
This is to be multiplied by LC to get circular scale reading.
Least count = value of 1 circular scale division =pitchnumber of division on circular scale
Length of rod A is chosen to match the ID(PQ) to be measured. Zero error is checked by taking reading between standard blocks fixed at normal value of ID to be measured. Zero error is positive if cap end is one the right of the main scale and negative it is on the left side.
_E01_259_Q02.png)
During zero setting of the above instrument, the end of the cap is on left side of the zero of main scale (i.e. zero of main scale is not visible) and 41th division of circular scale coincides with the reference line, the zero error is -
View Solution
Knowledge Check
Read the following statements and select the correct option.
Statement 1: Dental formula gives the number of teeth in the half of each jaw.
Statement 2: Dental formula can be expressed for insectivorous mammals as well as for the nonmammalian vertebrates.ABoth statements 1 and 2 are correctBStatement 1 is correct but statement 2 is incorrect Statement 1 is incorrect but statement 2 is correct.CStatement 1 is incorrect but statement 2 is correct.DBoth statements 1 and 2 are incorrect.The given figure shown the arrangement of different types of teeth in the jaw on one side. Identify A,B,C and D.
 AABCDInclisorsCaninePremolarsMolarsBABCDMolarsPremolarCaninesIncisorsCABCDPremolasrsMolarIncisorsCaninesDABCDIncisorsCanineMolarsPremolars
AABCDInclisorsCaninePremolarsMolarsBABCDMolarsPremolarCaninesIncisorsCABCDPremolasrsMolarIncisorsCaninesDABCDIncisorsCanineMolarsPremolarsA highly rigid cubical block A of mass M and side L is fixed rigidly on the another cubical block of same dimensions and of modulus of rigidity ρ such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the side faces of A. After the force is withdrawn, block A executes small oscillations, the time period of which is given by
A2π√MρLB2π√(Mρ/L)C2π√(ML/ρ)D2π√(M/ρL)
A highly rigid cubical block A of small mass M and side L is fixed rigidly on the other cubical block of same dimensions and of modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface . A small force F is applied perpendicular to one of the side faces of A. After the force is withdrawn , block A executes faces of A. After the force is withdrawn , block A exceutes small oscillations , the time period of which is given by
View SolutionMessages are conveyed by arranging four white, one blue, and three red flags on a pole. Flags of the same color are alike. If a message is transmitted by the order in which the colors are arranged, the total number of messages that can be transmitted if exactly six flags are used is a. 45 b. 65 c. 125 d. 185
View SolutionConsider a point charge q=1mC placed at a corner of a cube of sides 10 cm . Determine the electric flux through each face of the cube.
Strategy : We will learn about the utility of symmetry in solving problems with the help of Gauss's law . Here we'll use the symmetry of the situation,which involves the faces joining at the corner at which the charge resides.

(a) A charge q is placed atthe corner of a cube. (b) By surrounding the charge with a series of cubes such that the charge is at the centre of a larger cube, we have created an arrangement sufficiently symmetric to be able to solve for desired flux values.
You can see from figure that for these faces →E.ˆn=0. Since the normal is perpendicular to the surfaces while the electric field goes off in a spherically symmetric pattern and lies in the sides . In other words , the electric field that originates at the charge is tangential to the surface of these three sides. This means there is no flux through these sides. The electric flux through each of the remaining three faces of the be must be equal by symmetry . We'll referto these faces with the label F.
To fidn the flux through each of the sides F, we acan use a technique that puts the single charge in the middle of a larger cube. It takes seven other similarly placed cubes to surrounds the points charge q completely in figre. The charge is at the dead centre of the enw larger cube. So, the flux through each of the six sides of the large cube will now have an electric flux of one sixth of the total flux F. So given that the total structure is completely symmetric, the flux through a side F is one fourth of the flux through the larger side.
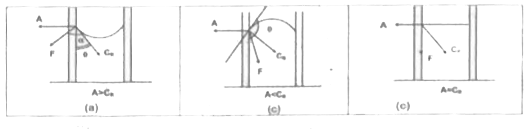
View SolutionThe force of interaction between the molecules of same substance is called cohesive force hile force of interaction between molecules of different substances is called adhesive force . Both the forces are attracive and have a range of about 10 A . If we consider a molecule . A well inside a liquid we find that it is equally attracted by the surrounding molecules in all the directions ( with a sphere of radius 10 Å ) and so it does not experience any resultant force . On or near the surface of a liquid , the molecules do not exist on the free side and so a molecule ( say B ) experiences a resultant force vertically downwards into the liquid . For this reason , the molecules of the surface have a tendency to go into the liquid . Thus , the surface tends to contract and gives rise to surface tension .
As surface molecules like B experience a net downward force of cohension and have tendency to go down , so in increasing the area of the surface more molecules are to be shifted to the surface from inside . Thus , more mechnical work will have to be done against the net downward force of cohension . This work is stored by the molecules in the surfaces as potential energy called free surface energy .
Furthermore , molcules like P , in contact with the liquid will stick to the solid surface , i.e will meet it if the force of adhesion A is greater than net force of cohension C . The liquid will not the solid surface if C>A
Also , molecules like Q at the surface in contact with the solid will experience a net force of cohension CR . If adhesion A is greater then cohension CR , the resultant force will be F . As the liquid can't support tangential force , F must be perpendicular to the surface of the liquid . So , the menisus will be concave and the angle of contact will be acute (>90∘) . However , if adhesion is lesser than cohension , the resultant force F will be directed into the liquid and so the menisus ( which is perpendicular to F as liquid support tangential force ) will be convex and the angle of contact will be obtuse (>90∘)
A liquid particle B , which is present in the vicinity particle A can exert a force on A if the distance of B from A is
View SolutionThe force of interaction between the molecules of same substance is called cohesive force hile force of interaction between molecules of different substances is called adhesive force . Both the forces are attracive and have a range of about 10 A . If we consider a molecule . A well inside a liquid we find that it is equally attracted by the surrounding molecules in all the dirctions ( with a sphere of radius 10 Å ) and so it does not experience any resultant force . On or near the surface of a liquid , the molecules do not exist on the free side and so a molecule ( say B ) experiences a resultant force vertically downwards into the liquid . For this reason , the molecules of the surface have a tendency to go into the liquid . Thus , the surface tends to contract and gives rise to surface tension .
As surface molecules like B experience a net downward force of cohension and have tendency to go down , so in increasing the area of the surface more molecules are to be shifted to the surface from inside . Thus , more mechnical work will have to be done against the net downward force of cohension . This work is stored by the molecules in the surfaces as potential energy called free surface energy .
Furthermore , molcules like P , in contact with the liquid will stick to the solid surface , i.e will meet it if the force of adhesion A is greater than net force of cohension C . The liquid will not the solid surface if C>A
Also , molecules like Q at the surface in contact with the solid will experience a net force of cohension CR . If adhesion A is greater then cohension CR , the resultant force will be F . As the liquid can't support tangential force , F must be perpendicular to the surface of the liquid . So , the menisus will be concave and the angle of contact will be acute (>90∘) . However , if adhesion is lesser than cohension , the resultant force F will be directed into the liquid and so the menisus ( which is perpendicular to F as liquid support tangential force ) will be convex and the angle of contact will be obtuse (>90∘)

The free suface energy , stored in the surface is because of work done
View Solution
