In the figure, the pulley P moves to the right with a constant speed u. The downward spee of A is vA and the speed of B to the right is vB . Then,
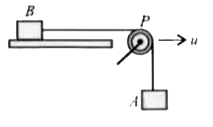
vA=vB
vB=u+vA
vB+u=vA
the two blocks have accelerations of the same magnitude.
The correct Answer is:B, D
At any instant of time, let the length of the string BP=l1 and the length PA=l2 . In a further time t, let B move to the right by x and A move down by y, while P moves to the right by ut. As the length of the string must remain constant ,
l1+l2=(l1−x+ut)+(l2+y)
orx=ut+yordxdt=u+dydt
dxdt = speed of B to the right =vB
dydt = downward speed of A =vA∴vB=u+VA
Also dvBdt=dvAdt=oraB=aA
Topper's Solved these Questions
- MODEL TEST PAPER 1 BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 1 EXERCISE - PHYSICS (Category) 2 : Single Option correct type (2 mark)
5 Videos
- MAGNETICSBOOK - MTG-WBJEECHAPTER - MAGNETICSEXERCISE - WB JEE Previous Years Questions (Category 3: One or More than one Option)
2 Videos
- MODEL TEST PAPTER BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPTER EXERCISE - MCQs
80 Videos
Similar Questions
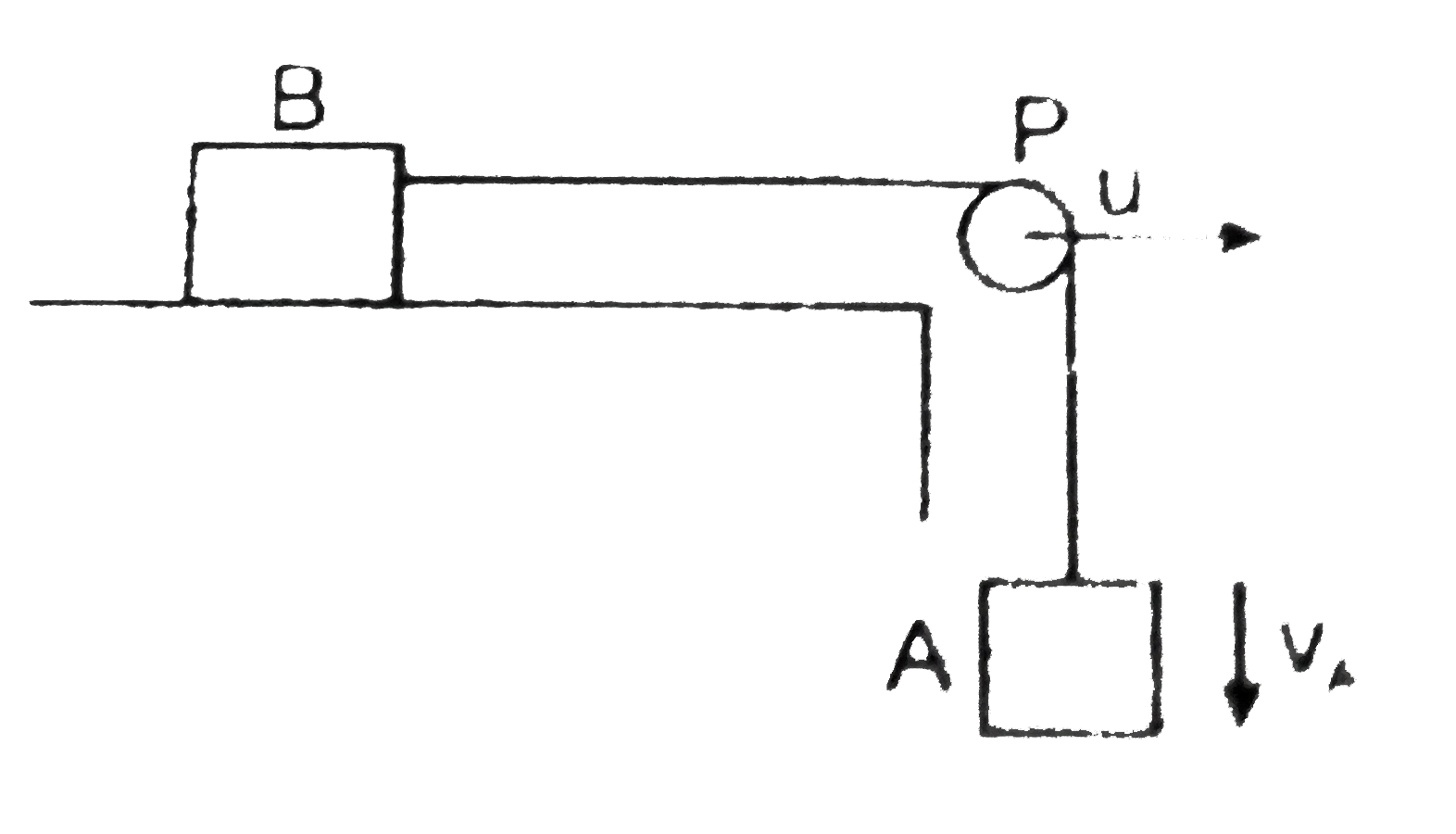
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.
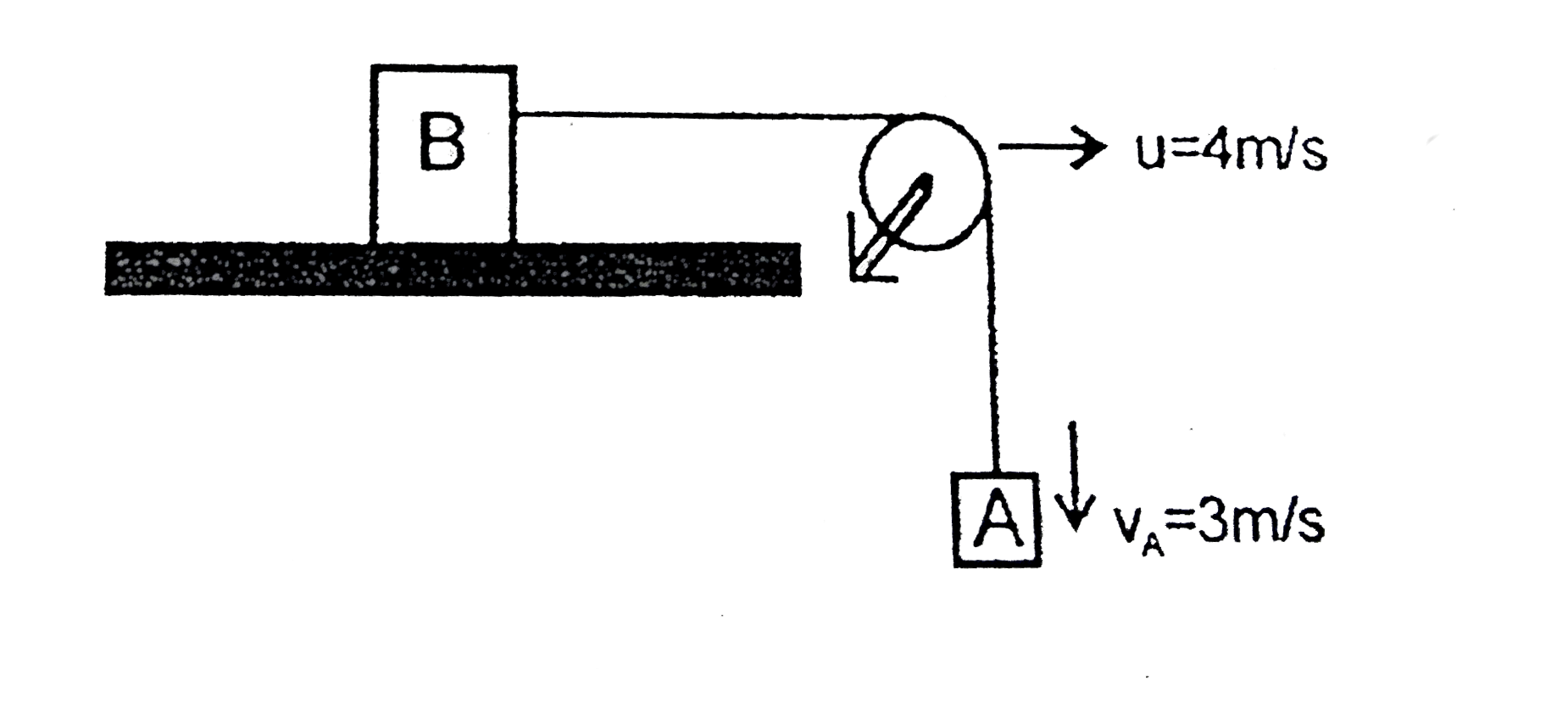
View SolutionIn the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
View Solution
Knowledge Check
In the figure, the pulley P moves to the right with a constant speed u. The downward speed of A is vA, and the speed of B to the right is vB.
 AvB=vABvB=u+vACvB+u=vADThe two blocks have accelerations of the same magnitude.
AvB=vABvB=u+vACvB+u=vADThe two blocks have accelerations of the same magnitude.In the figure, the pulley P moves to the right with a constant speed u. The downward speed of A is vA, and the speed of B to the right is vB :
 AvB=u+uABvB+u=vACvA=vBDThe two blocks have acceleration of the same magnitude
AvB=u+uABvB+u=vACvA=vBDThe two blocks have acceleration of the same magnitude
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.AVB=VABVB=u+VACVB+u=VADthe two blocks have acceleration of the same magnitude.
In the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).

View Solution
In the figure, the pulley P moves to the right with a constant speed v0. If the velocity of B is v in downward direction, find the velocity of A.
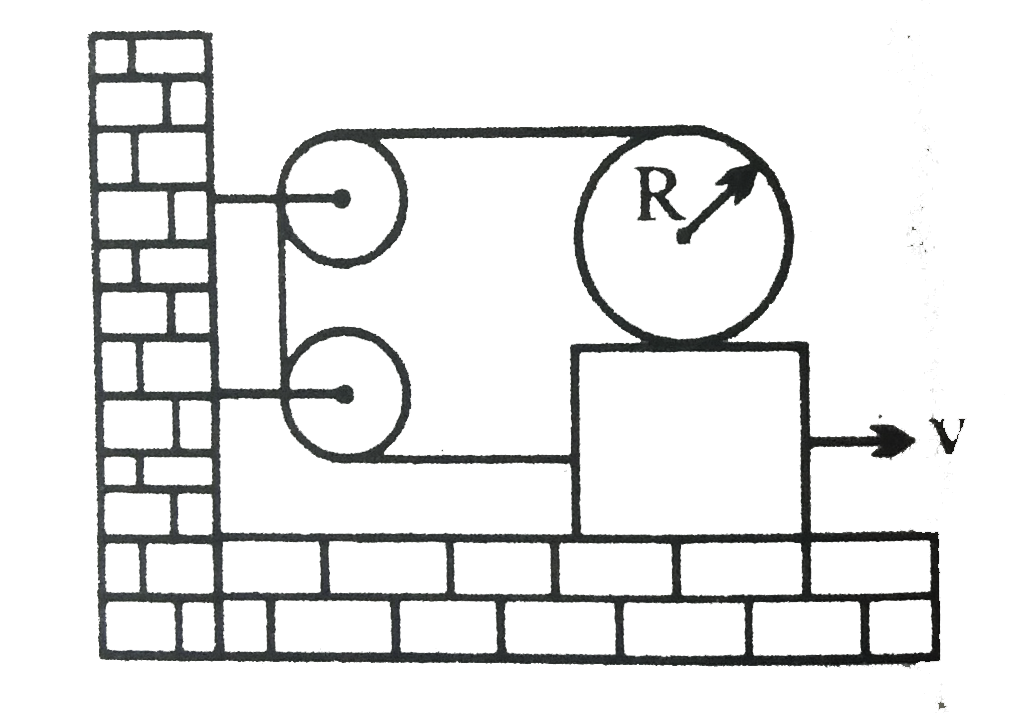
View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
 .
.
View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
 .
.
View SolutionIn the figure find the speed of pulley P

View Solution
