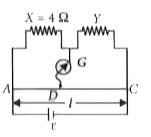
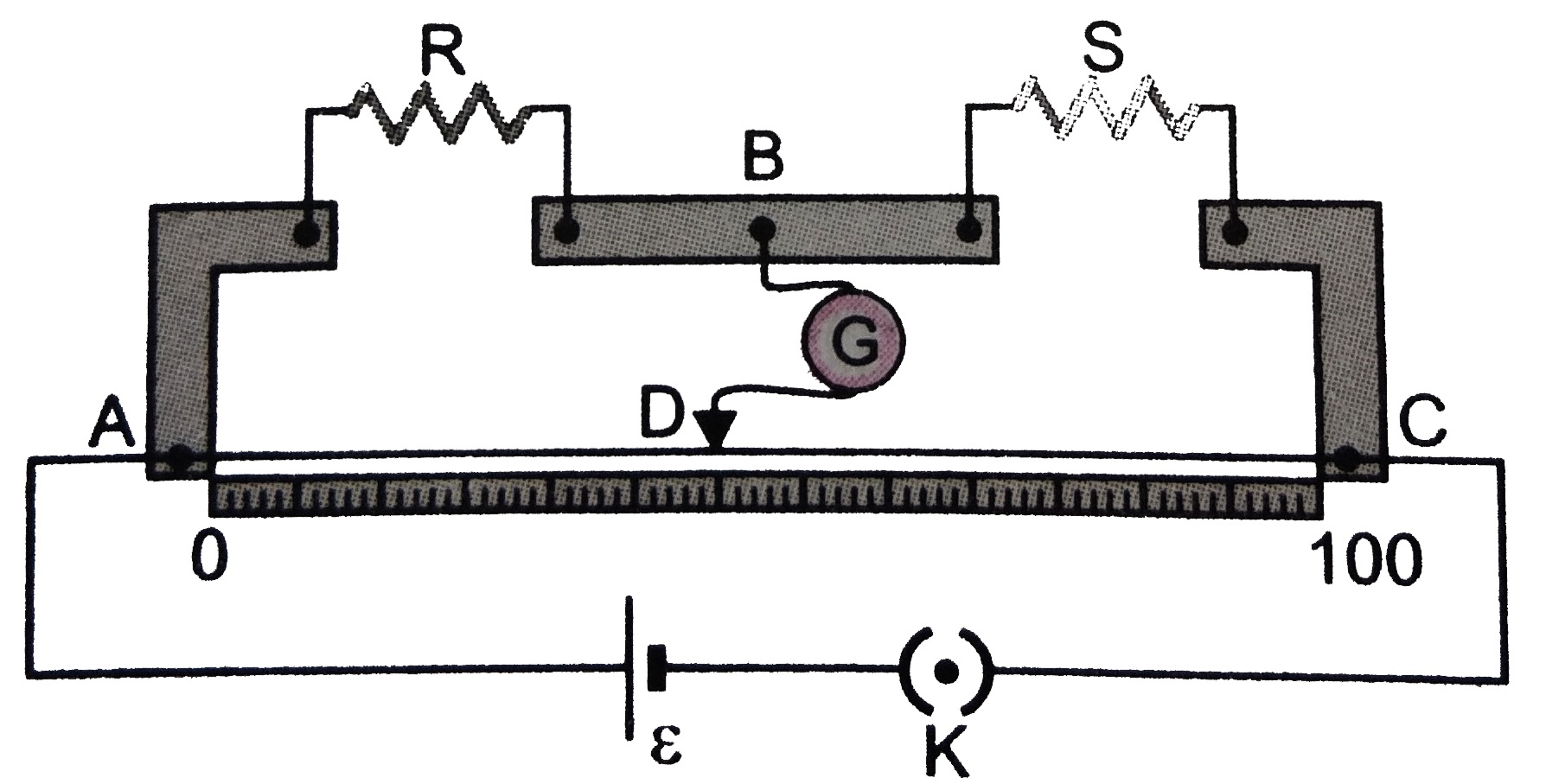
Figure shows a meter bridge, wire AC has uniform cross section. The length of wire AC is 100 cm X is a standard do resistor of 4 Ω and Y is a coil. When Y is immersed in melting ice, the null point is at 40 cm from point A. When the coil Y is heated to 100∘C, a 100 Ω resistor has to be connected in parallel with Y in order to keep the bridge balanced at the same point. Temperature coefficient of resistance of the coil is
6.3×10−4K−1
4.3×10−4K−1
8.3×10−4K−1
2.3×10−4K−1
The correct Answer is:A
XR0=1100−l=4060,R0=6Ω
Since null point remains unchanged xR.=4060
6=100RtRt+100,Rt=6.38Ω
∴α=Rt−R0R0Δt=6.3×10−4K−1
Topper's Solved these Questions
- MODEL TEST PAPER 1 BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 1 EXERCISE - PHYSICS (Category) 3 : Single Option correct type (2 mark)
5 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
Similar Questions
The figure shows a meter bridge wire AC having unifrom area o cross-section. X is a standard resistance of 4Ω and Y is a resistance coil. When Y is immersed in melting ice the null point is at 40 cm from point A. when the coil Y is heated to 100∘ C, a resistance of 100Ω has to be connected in parallel with Y, in order to kkep the bridge balanced at the sam point. The temperature coefficient of resistance of coil is
View SolutionAs shown in the figure, a meter bridge consisting of two resistances P and Q together in parallel with a meter-long wire AB of uniform cross-section. C is a movable contact that can slide along the wire AB. The resistors P,Q and resistances of segments AC and CB of the wire constitude the four arms of bridge. the length AB=100cm,P=4Ω,Q is a coil of wire. With Q immersed in melting ice the null point is found to be at a distance of 40cm from A. When the coil Q is heated to 100∘C, a 100Ω resistor has to be connected in parallel with Q in order to keep the bridge balanced at teh same point. Calculate the temperature coefficient of resistance of the coil.
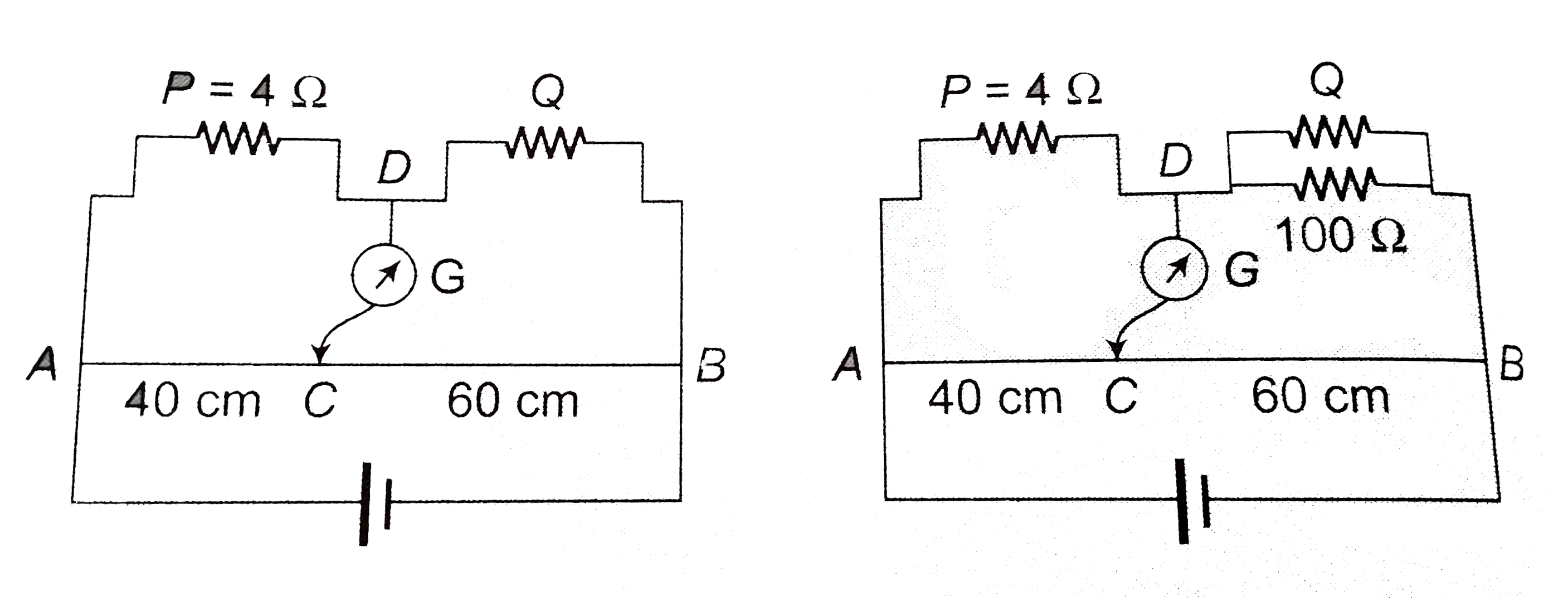 .
.
View Solution
Knowledge Check
In a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
 A15ΩB12ΩC10ΩD5Ω
A15ΩB12ΩC10ΩD5Ω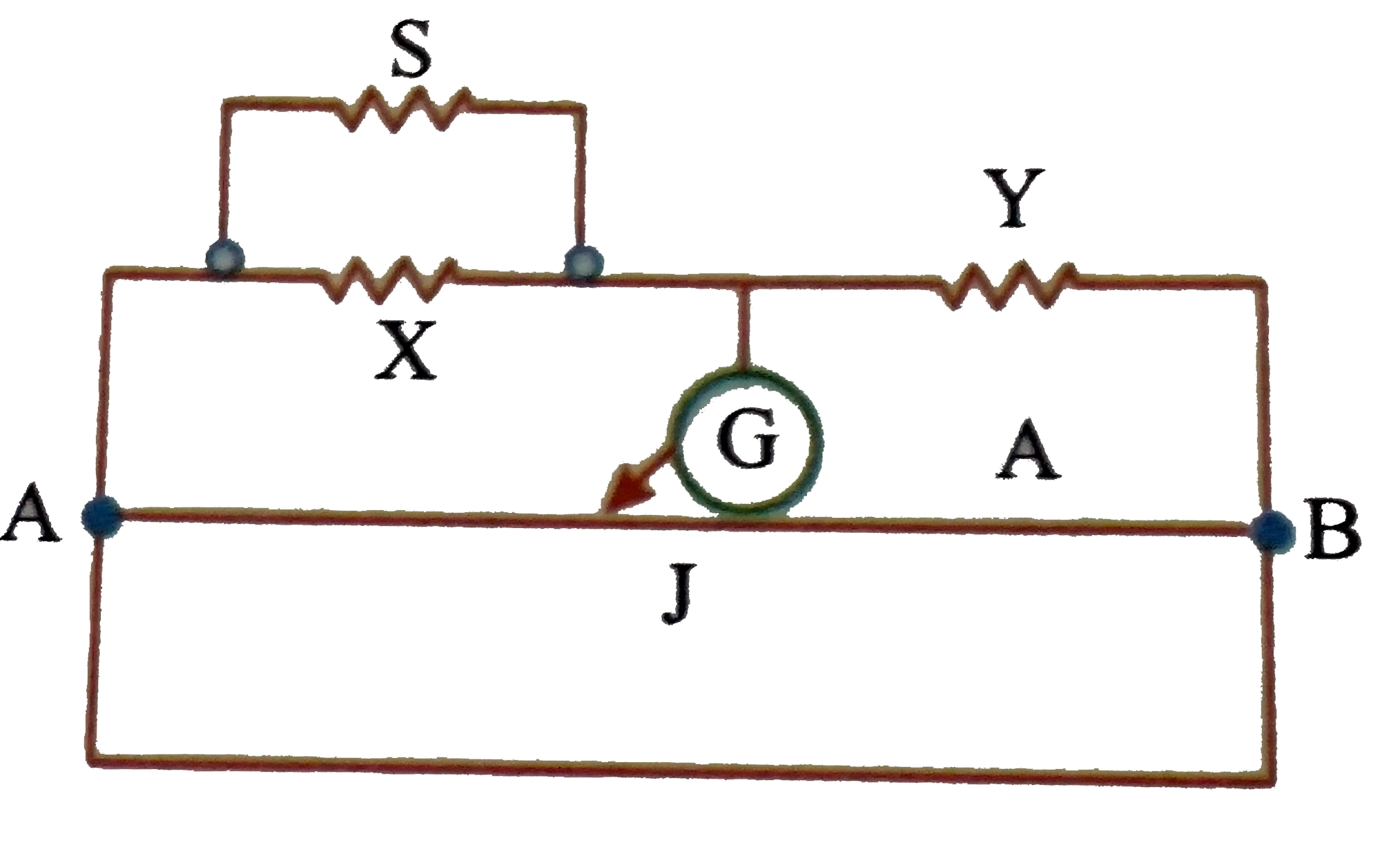
In the meter bridge experiment, the length Ab of the wire is 1m. The resistors X and Y have values 5Ω and 2Ω respectively. When a shunt resistance S is connected to X, the balacing point is found to be 0.625 m from A. Then the resistance of the shunt isA5ΩB10ΩC7.5ΩD12.5Ω
In a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn a meter bridge,
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View SolutionIn a meter bridge,

the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
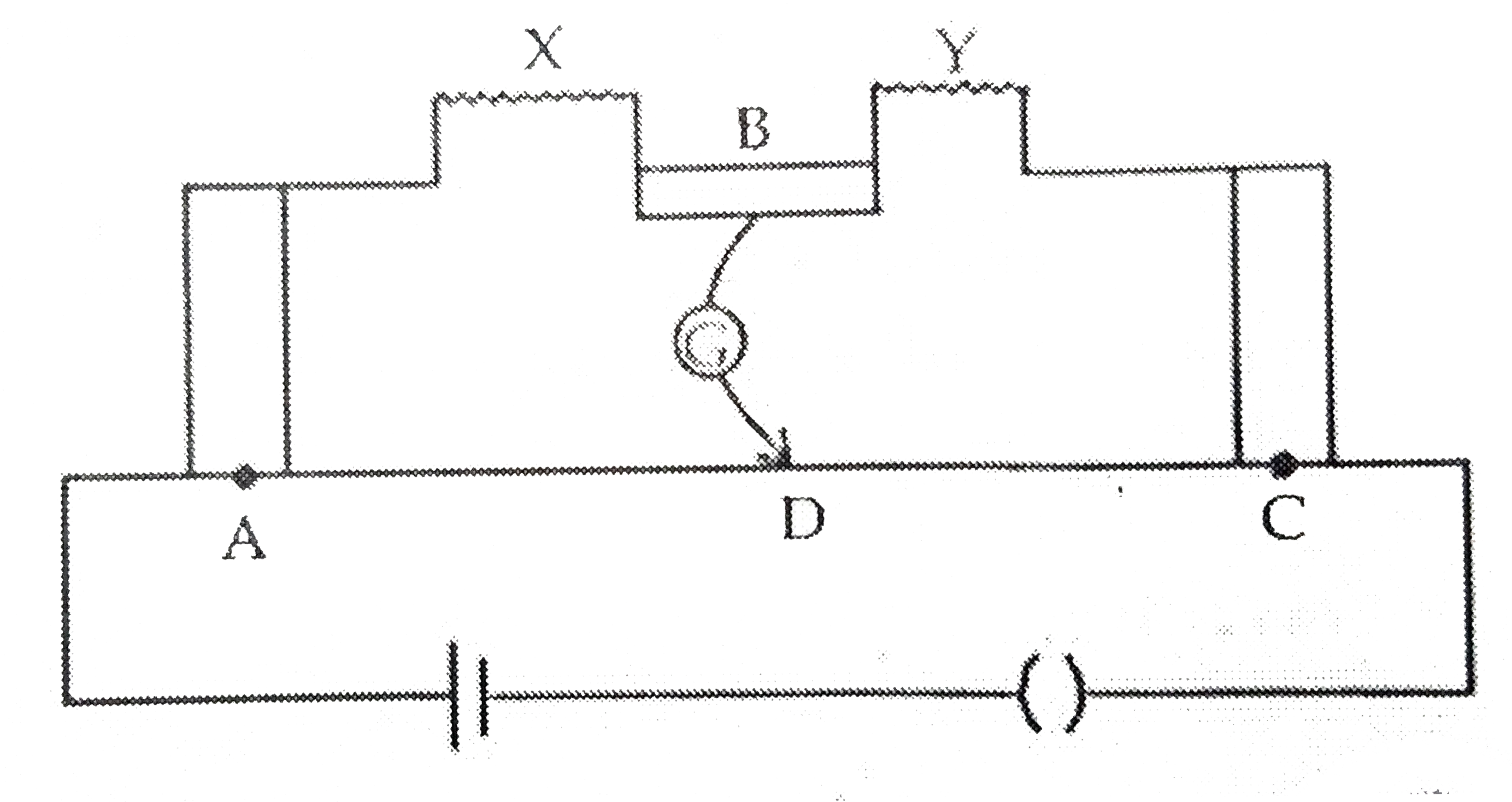
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View Solution

