The differential equation of charging of a capacitor is as given below:
1K1dqdt+K2q=K3
The time constant and steady state charge are respectively
A
1K1 and K3
B
1K1K2 and K3K2
C
K2K1 and K2K3
D
1K1K2 and K3K1
Text Solution
The correct Answer is:B
Consider the circuit
ε−qC−IR=0
I=dqdt
Now, εC=dqdt.RC+q
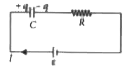
⇒RCdqdt+q=εC [where , q0=Cε] …(i)
Comparing eq. (i) with 1K1.dqdt+K2q=K3, we get
τ=1K1K2,q0=K3K2
|
Topper's Solved these Questions
- MODEL TEST PAPER 1 BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 1 EXERCISE - PHYSICS (Category) 3 : Single Option correct type (2 mark)
5 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
Similar Questions
Knowledge Check
The circuit is in a steady state.
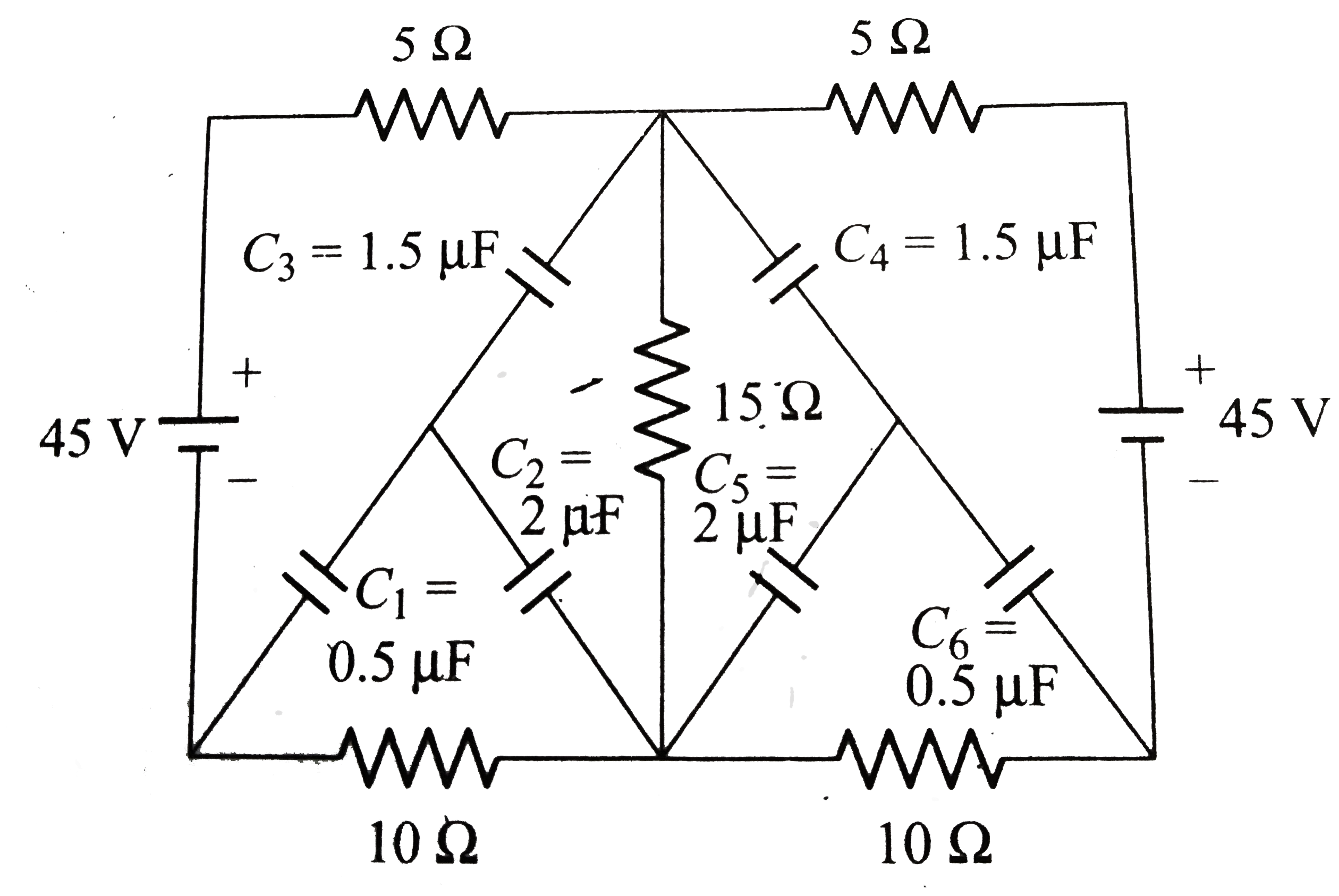
The charge in capacitor C1 isA20μCB30μCC40μCD10μCThe circuit is in a steady state.
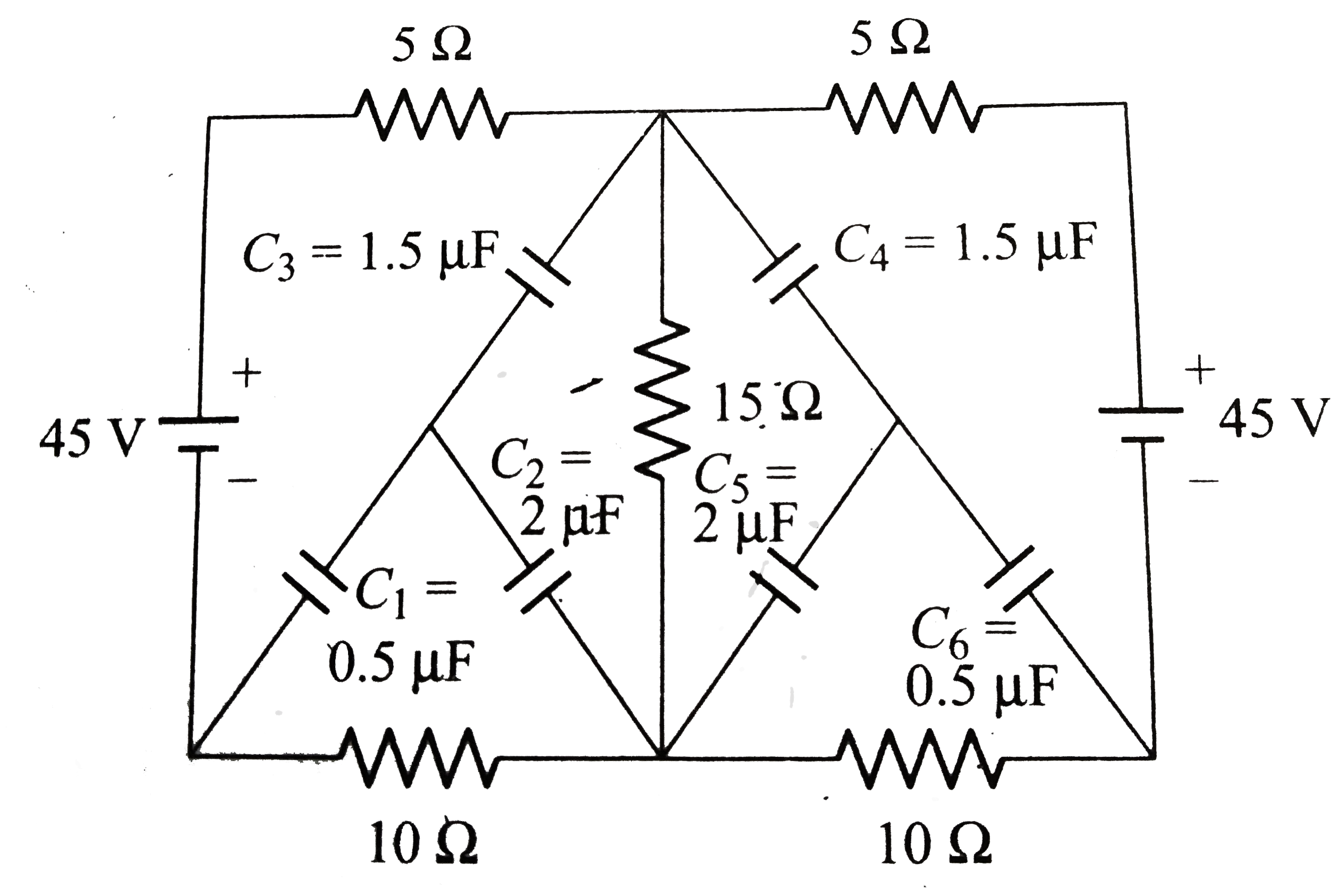
The charge in capacitor C3 isA10μCB30μCC20μCD40μCThe circuit is in a steady state.
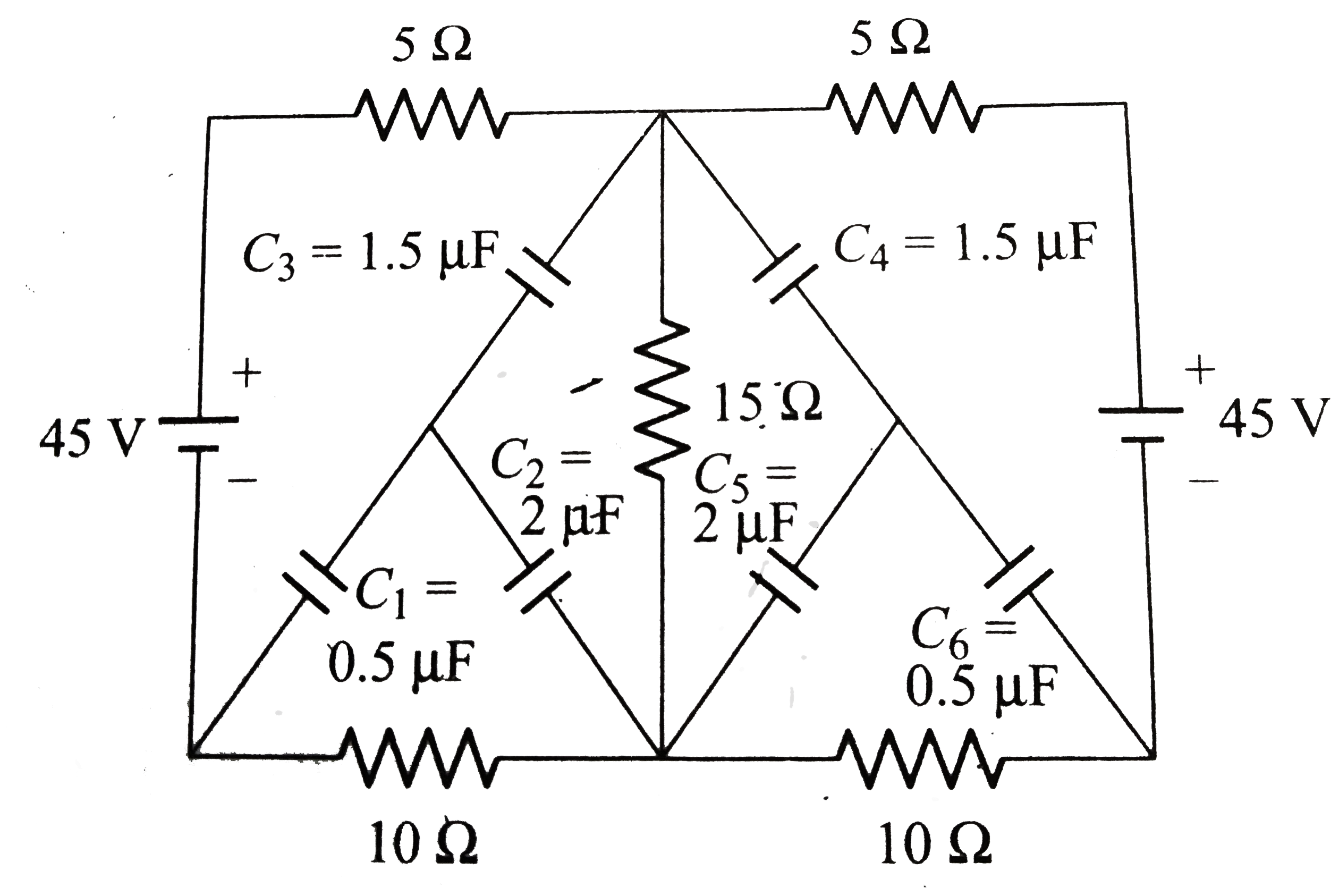
The charge in capacitor C2 isA30μCB10μCC20μCD40μC
The circuit is in a steady state.

The charge in capacitor C2 is
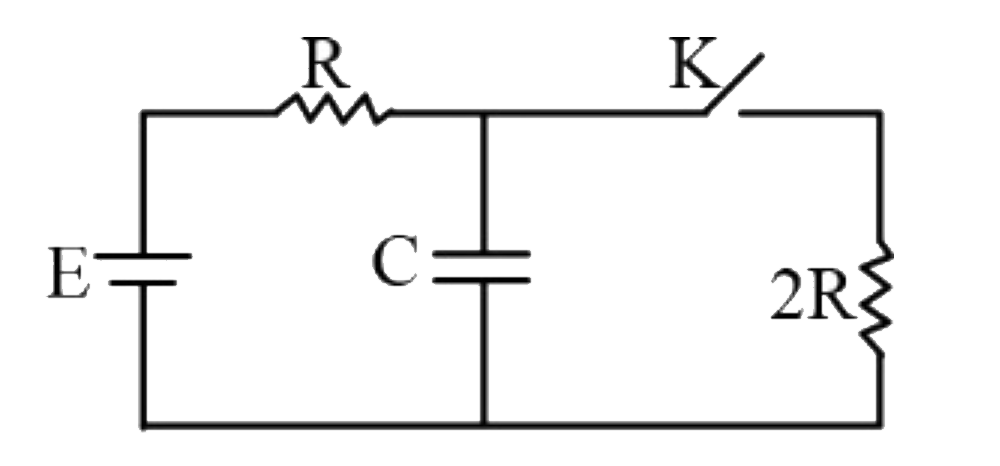
View SolutionIn the given circuit switch K is open. The charge on the capacitor is C is steady-state is q1 Now the key is closed and steady-state charge on C is q2 The ratio of charges q1/q2 is -
View SolutionThe electrostatic force between two charges Q1andQ2 at separation r is given by F=K.Q1Q2r2 The constant K
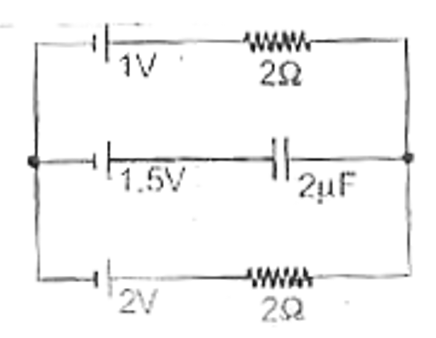
View SolutionThe charge in the 2μF capacitor at steady state is
View SolutionIn the given circuit switch K is open. The charge on the capacitor is C is steady-state is q1 Now the key is closed and steady-state charge on C is q2 The ratio of charges q1/q2 is -

View Solution
