What is the resistance of one of the rails of a railway track 20 km long at 20∘C? The cross section area of rail is 25 cm2 and the rail is made of steel having resistivity at 20∘ C as made of steel having resistivity at 20∘ C as 6×10−8Ωm.Solution in Marathi
Step by step video & image solution for What is the resistance of one of the rails of a railway track 20 km long at 20^@C? The cross section area of rail is 25 cm^2 and the rail is made of steel having resistivity at 20^@ C as made of steel having resistivity at 20^@ C as 6 xx 10^-8 Omegam. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Light year is a unit of
View SolutionWhich types of waves are used in different Electronic gadgets?
View SolutionA rail track made of steel having length 10m is clamped on a railway line at its two end (figure). On a summer day due to rise in temperatue by 20∘C. It is deformed as shown in figure. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C

View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
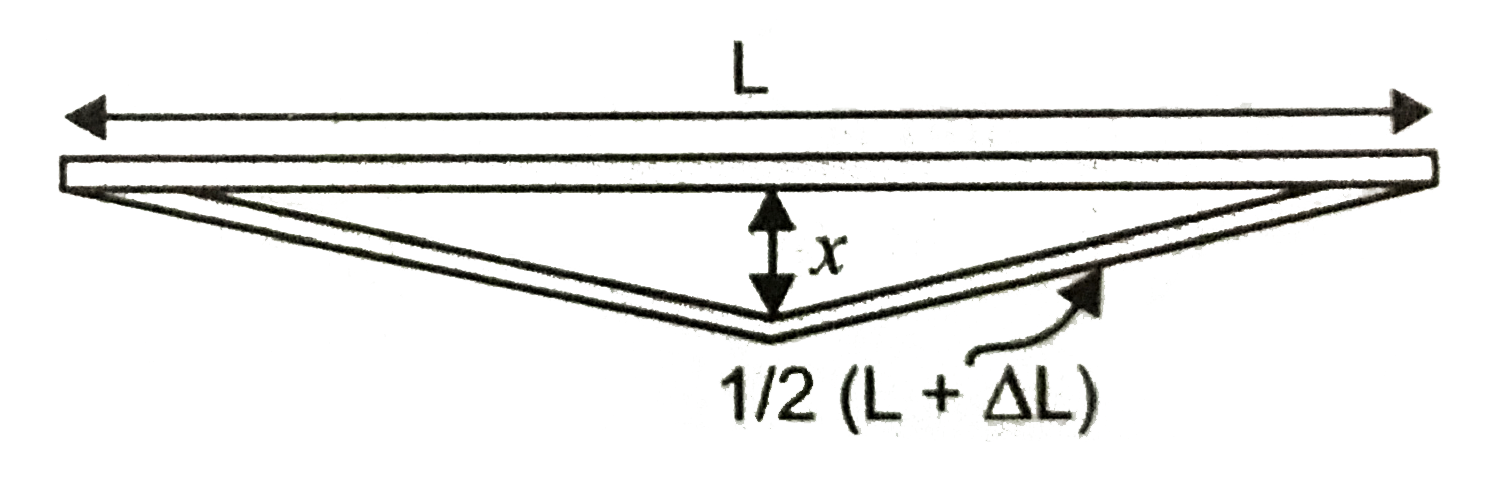
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends as shown in figure. On a summer day due to rise in temperature by 20∘C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel=1.2×10−5 ∘C−1
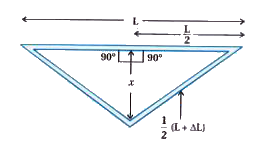
View SolutionTwo materials have the value of α1andα2 as 6×10−4(∘C)−1and−5×10−4(∘C)−1
respectively. The resistivity of the first material ρ20=2×20−8Ω. A new material is made by combining the above two materials. the resistivity does not change with temperature . The resistivity ρ20 of the second material is .... Considering the reference temperature as 20∘C assume that the resistivity of the new material is equal to the sum of the resistivity of its component materials.
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends on a summer day due to rise in temperature by 20^@C, it is deformed as shown in fig. Find x (displacement of the centre) if alpha_(steel) = 1.2 xx 10^(-5)//^@C.
View SolutionA rail track made of steel having length 410 mis clamped on a raillway line at its two ends ( Fig 11.3 ). On a summer day due to rise in temperature by 20∘ C , it is deforned as shown in figure. Find x (displacement of the centre) if
αsteel=1.2×10−5/∘C
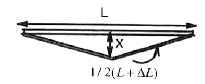
View Solution10 m लंबी स्टील की बनी रेल की पटरी किसी रेलवे लाइन पर अपने दोनों सिरों पर जकड़ी है (चित्र 11.3)। किसी गर्मी के दिन ताप में 20∘C की वृद्धि होने पर यह आकृति में दर्शाय अनुसार विरूपित हो जाती है। यदि αsteel=1.2×10−5/∘C है तो x का मान (केंद्र का विस्थापन) ज्ञात कीजिए।
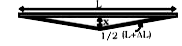
View SolutionAt 20^@C , the gap between the rails each 50 m in length is observed to be 1.65 cm. If the lines are made of steel (alpha = 11 xx 10^-6 //^@C) , at what temperature will the lines just touch?
View SolutionRailway lines are laid with gaps to allow for expansion. If each line is 10 m long at 20^@C , what should be the length of the gap to be kept between two rails to allow for expansion if the maximum temperature that can be reached is 50^@C ? (alpha_(steel)=1.2 xx 10^-6//^@C)
View SolutionRailway tracks are laid with gaps for expansion. The gap between the steel rails 20 m long is 1.2 cm at 10∘C. The temperature at which the steel rails just touch each other is (∝steel=12×10−6/∘C)
View SolutionCalculate the length of an aluminium wire of diameter 0.4 mm required to have a resistance of 2 Omega at 20 ^@C . Resistivity of aluminium is 2.8 xx 10^-8Omegam .
View Solution500 मी लम्बी स्टील से बनी रेल की पटरियाँ 20∘C पर लगाई गई हैं। दो पटरियों के बीच कितना स्थान छोड़ा जाए यदि अधिकतम सम्भावित ताप 50∘C है? (स्टील का रेखीय प्रसार गुणांक =11×10−6/∘C)
View SolutionSteel railroad tracks are laid when the temp is 20∘C. A standard section of rail is 12m long. Calculate the gap that should be left between rail sections so that there may not be any compression when the temperature gets as high as 50∘C. (α of steel = 11×10−6per∘C)
View Solution
