What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution ? Take the radius of the wheel as R and the x-axis as the forward direction?
From figure , during half revolution of the wheel , the point A covers πR(=AC) horizontal distance while 2R(=BC) vertical distance
so here , P=πR,Q=2R
∴Displacement,b=√P2+Q2
=√(πR2)+(2R)2=R√π2+4
and θ=nTan−1(QP)=Tan−1(2RπR)=Tan−1(2π)with x-axis.
i.e., Displacement has magnitude R√π2+4 and makes an angle Tan−1(2π)with x-axis.

Topper's Solved these Questions
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Short Answer type question
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Very Short Answer type Questions
8 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution ? Take the radius of the wheel as R and the the x - axis as the forward direction ?
View SolutionA wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View Solution
Knowledge Check
The displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward quarter revolution where perimeter of the wheel is 4πm, is (Assume the forward direction as x-axis)
A√(π+2)2+4along tan−12π with x-axisB√(π+2)2+4along tan−12π−2 with x-axisC√(π+2)2+4along tan−12π with x-axisD√(π+2)2+4along tan−12π−2 with x-axisThe radius of a wheel is 3.5 cm. What is the distance (in cm.) travelled by the wheel in 20 revolutions ?
AA)220BB)440CC)880DD)1320A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
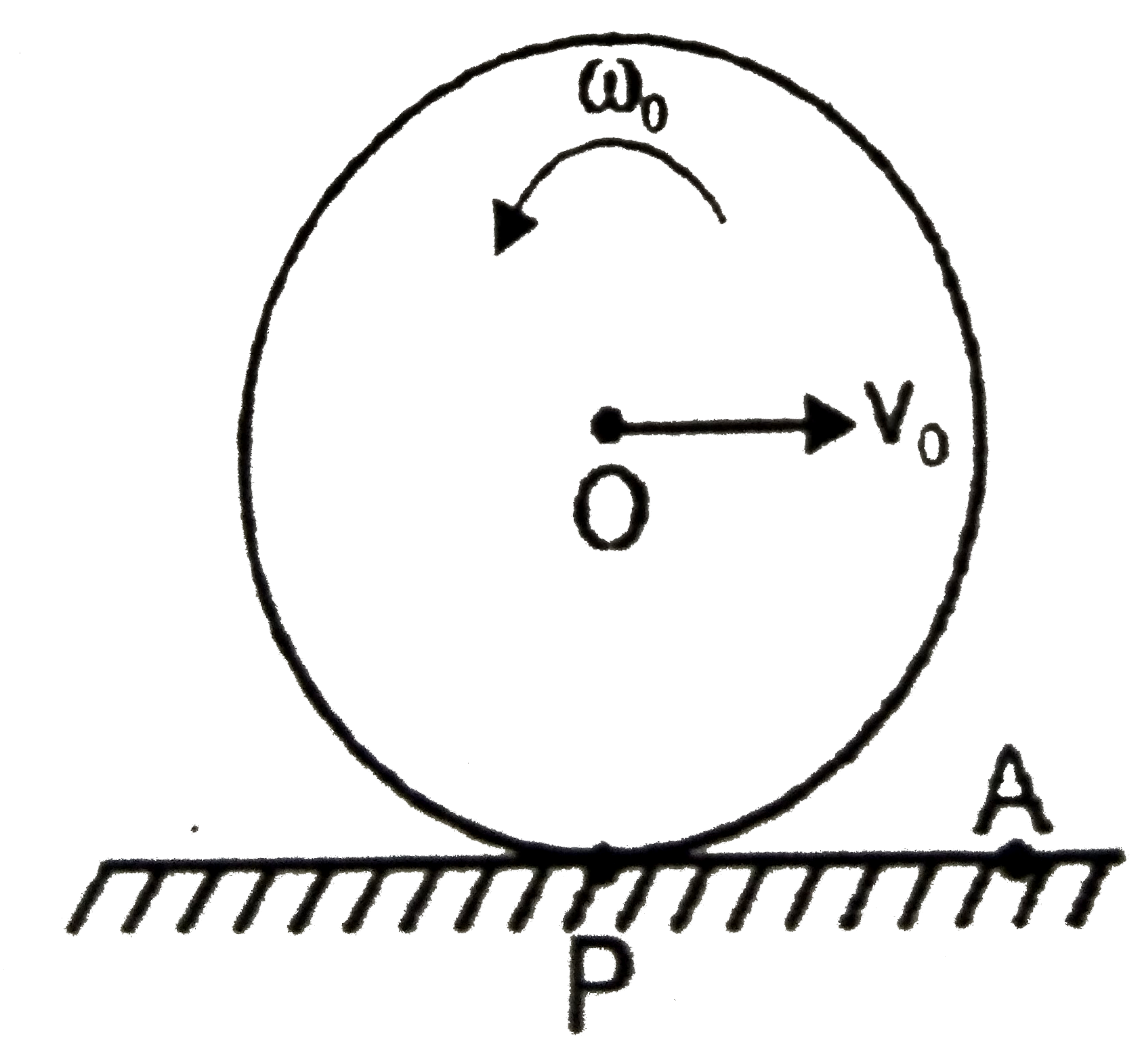
If the wheel comes to permanent rest after sometimes, then :Av0=ω0rBv0=ω0k2rCv0=ω0r2RDV0=ω0(r+k2r)
A Wheel of circumference C is at rest on the ground.When the wheel rolls forward through half a revolution ,then the displacement of point contact will be
View SolutionA wheel of perimeter 4π is rolling on a horizontal surface. The displacement of the point of contact of wheel and ground when the wheel completes one quarter of revolution is
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
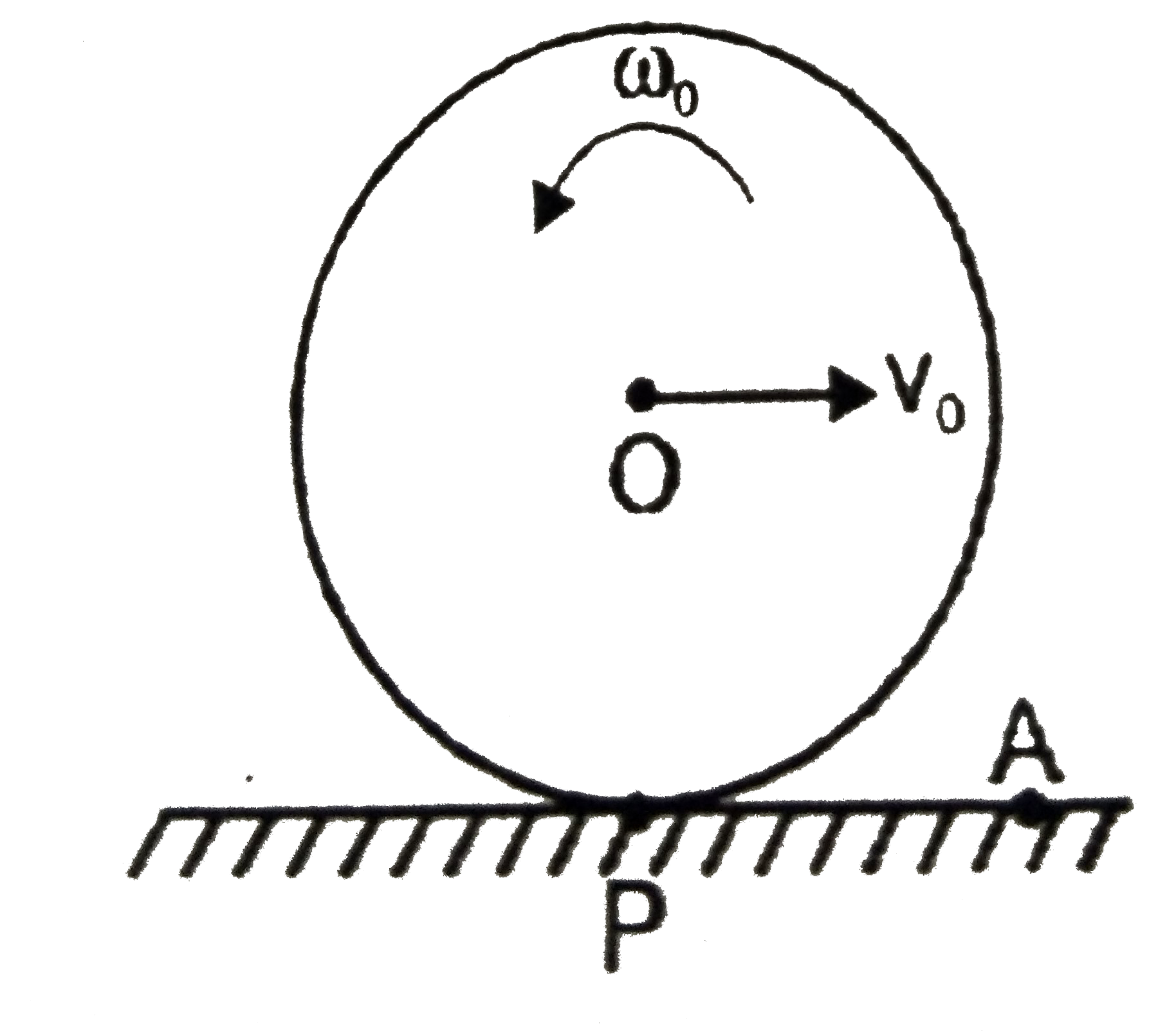
If above question , distance travelled by centre of mass of the wheel before it stops is −
View Solution
